Question

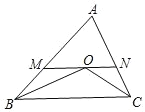
【题目】如图，在△ABC 中，∠ABC、∠ACB 的角平分线交于点 O，MN 过点 O，且MN∥BC，分别交 AB、AC 于点 M、N．若 MN=5cm，CN=2cm，则 BM=________cm．

Answer 1

【答案】3cm

【解析】

根据角平分线的定义及平行线的性质证得∠MBO=∠MOB、∠NOC=∠OCN，根据等腰三角形的判定方法可得BM=MO，ON=CN，由MN=MO+ON=BM+CN即可求得BM的长.

∵∠ABC、∠ACB 的平分线相交于点 O，

∴∠MBO=∠OBC，∠OCN=∠OCB，

∵MN∥BC，∴∠OBC=∠MOB，∠NOC=∠OCB，

∴∠MBO=∠MOB，∠NOC=∠OCN，

∴BM=MO，ON=CN，

∴MN=MO+ON，即 MN=BM+CN，

∵MN=5cm，CN=2cm，

∴BM=5﹣2=3cm.

故答案为 3cm．