题目内容
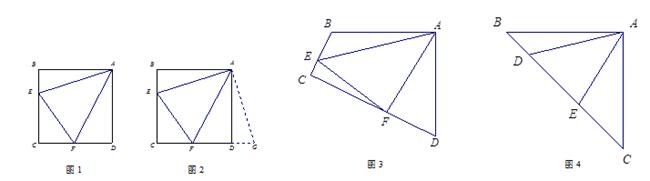
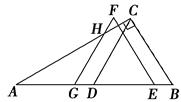
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )


A.10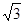 -15 -15 | B.10-5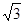 |
C.5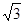 -5 -5 | D.20-10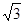 |
D
根据轴对称的性质可得AE=ED,在Rt△EDC中,利用60度角求得ED=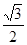 CE,列出方程CE +ED=(1+
CE,列出方程CE +ED=(1+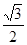 )EC=5,解方程即可求解.
)EC=5,解方程即可求解.
解:∵AE=ED
在Rt△EDC中,∠C=60°,ED⊥BC
∴ED=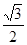 EC
EC
∴CE+ED=(1+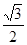 )CE =5
)CE =5
∴CE=20-10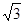 .
.
故选D.
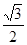 CE,列出方程CE +ED=(1+
CE,列出方程CE +ED=(1+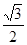 )EC=5,解方程即可求解.
)EC=5,解方程即可求解.解:∵AE=ED
在Rt△EDC中,∠C=60°,ED⊥BC
∴ED=
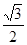 EC
EC∴CE+ED=(1+
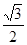 )CE =5
)CE =5∴CE=20-10
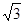 .
.故选D.

练习册系列答案
相关题目