题目内容
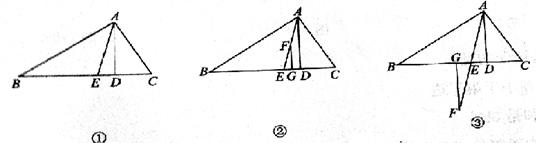
已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
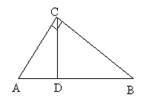
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
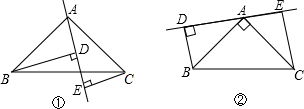
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
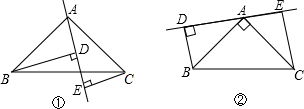
(1)见解析 (2)见解析 (3)BD=DE-CE
此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,利用了转化及等量代换的思想,熟练掌握全等三角形的判定与性质是解本题的关键.
(1)由BD垂直于AE,得到三角形ABD为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由∠BAC=90°,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,AB=AC,利用AAS可得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=AD+DE,等量代换即可得证;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系为BD=DE-CE,理由为:同(1)得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=DE-AD等量代换即可得证;
(3)由(1)(2)总结得到当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
解:(1)证明:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,
∵∠BAC=90°,∴∠BAD+∠EAC=90°∴∠ABD=∠EAC,
在△ABD和△CAE中
∵
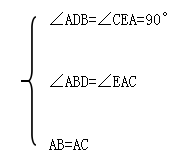
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD、DE、CE的关系为BD=DE-CE,理由为:
证明:在△ABD和△CAE中
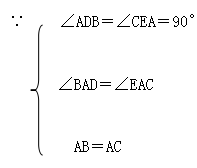
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=DE-AD,
∴BD=DE-CE;
(3)当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
(1)由BD垂直于AE,得到三角形ABD为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由∠BAC=90°,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,AB=AC,利用AAS可得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=AD+DE,等量代换即可得证;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系为BD=DE-CE,理由为:同(1)得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=DE-AD等量代换即可得证;
(3)由(1)(2)总结得到当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
解:(1)证明:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,
∵∠BAC=90°,∴∠BAD+∠EAC=90°∴∠ABD=∠EAC,
在△ABD和△CAE中
∵

∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD、DE、CE的关系为BD=DE-CE,理由为:
证明:在△ABD和△CAE中

∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=DE-AD,
∴BD=DE-CE;
(3)当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,
,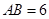 ,
,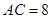 ,点
,点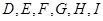 都是矩形
都是矩形 的边上,则矩形
的边上,则矩形

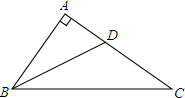

 -15
-15