题目内容
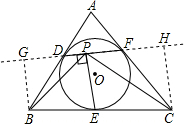
如图,已知:⊙O是ABC的内切圆,切点分别为D,E,F,连接DF,作EP⊥DF,垂足为点P,连接PB,PC.求证:∠DPB=∠FPC.
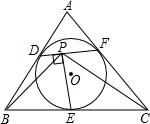

证明:分别过B、C作DF的垂线交DF延长线于G、H两点,
∵⊙O是ABC的内切圆,切点分别为D,E,F,
∴BE=BD,CF=CE,AD=AF,
∴∠ADF=∠AFD,
∴∠BDG=∠CFH,
又∵∠G=∠H=90°,
∴△BDG∽△CFH,
∴
=
,
∴
=
,
∵∠G=∠EPG=∠H=90°,
∴BG∥EP∥CH,
∴
=
,
∴
=
,
又∵∠G=∠H=90°,
∴△BGP∽△CHP,
∴∠DPB=∠FPC.
∵⊙O是ABC的内切圆,切点分别为D,E,F,
∴BE=BD,CF=CE,AD=AF,
∴∠ADF=∠AFD,
∴∠BDG=∠CFH,
又∵∠G=∠H=90°,
∴△BDG∽△CFH,
∴
| BG |
| CH |
| BD |
| CF |
∴
| BG |
| CH |
| BE |
| CE |
∵∠G=∠EPG=∠H=90°,
∴BG∥EP∥CH,
∴
| BE |
| CE |
| PG |
| PH |
∴
| BG |
| CH |
| PG |
| PH |
又∵∠G=∠H=90°,
∴△BGP∽△CHP,
∴∠DPB=∠FPC.


练习册系列答案
相关题目