题目内容
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N.
(1)观察图1,直接写出∠AEM与∠BNE的关系是;(不用证明)
(2)如图1,当M、N都分别在AB、BC上时,可探究出BN与AM的关系为:;(不用证明)
(3)如图2,当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式是否仍然成立?若成立,请说明理由:若不成立,写出你认为成立的结论,并说明理由.
【答案】
(1)∠AEM+∠BNE=90°
(2)BN⊥AM,BN﹣AM=2
(3)
解:当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式仍然成立.
证明:如图2,
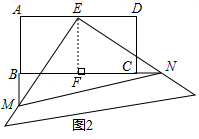
∵四边形ABCD为矩形,
∴BN⊥AM,
过E作EF⊥BC于F
∵矩形ABCD中,AD=2AB=4,E是AD的中点,
∴AE=EF=AB=BF=2,
∵∠AEM+∠MEF=90°,∠NEF+∠MEF=90°,
∴∠AEM=∠FEN,
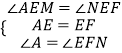 ,
,
∴Rt△AEM≌Rt△FEN,
∴AM=FN,
∴BN﹣AM=BN﹣FN=BF=2.
【解析】解:(1.)∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEN=∠BNE,
∵∠MEN=90°,
∴∠AEM+∠DEN=90°,
∴∠AEM+∠BNE=90°,
故答案为:∠AEM+∠BNE=90°;
(2.)BN⊥AM,BN﹣AM=2;
证明:如图1,∵四边形ABCD为矩形,
∴BN⊥AM,
过E作EF⊥BC于F,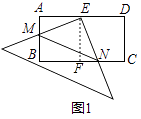
∵矩形ABCD中,AD=2AB=4,E是AD的中点
∴AE=EF=AB=BF=2,
∵∠AEM+∠MEF=90°,∠NEF+∠MEF=90°,
∴∠AEM=∠NEF,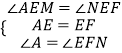 ,
,
∴Rt△AEM≌Rt△FEN,
∴AM=FN,
∴BN﹣AM=BN﹣FN=BF=2;
故答案为:BN⊥AM,BN﹣AM=2;
(1)由矩形的性质可得AD∥BC,由平行线的性质定理可得∠DEN=∠BNE,由∠MEN=90°,易得∠AEM+∠DEN=90°,可得∠AEM+∠BNE=90°;(2)由矩形的性质可得BN⊥AM,过E作EF⊥BC于F,由E是AD的中点可得,AD=2AB=4,易得AE=EF,易得Rt△AEM≌Rt△FEN,由全等三角形的性质可得AM=FN,易得BN﹣AM=BN﹣FN=BF=2;(3)同(2)可证得结论.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案




