题目内容
【题目】 如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
(1)求证:PD是⊙O的切线;
(2)如图2,点M是 ![]() 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A= ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:连结OD;

∵AB是⊙O的直径,
∴∠ADB=90°,OA=OB,∠A+∠ABD=90°;
又∵OA=OB=OD,
∴∠ADO=∠A,∠BDO=∠ABD;
又∵∠A=∠PDB,
∴∠PDB+∠BD0=90°,
即∠PDO=90°,且D在圆上,
∴PD是⊙O的切线;
(2)解:连结OM,过D作DF⊥AB于F;
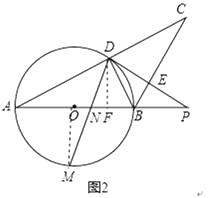
∵点M是 ![]() 的中点,
的中点,
∴OM⊥AB;设BD=x,
∵tan∠A= ![]() =
= ![]() ,
,
∴AD=4x;由勾股定理得:
AB= ![]() =
= ![]() x;由三角形的面积公式得:
x;由三角形的面积公式得: ![]() ADBD=
ADBD= ![]() ABDF,
ABDF,
∴DF= ![]() x,
x,
∵OM∥DF,
∴△OMN∽△FDN,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连结OD;由AB是⊙O的直径,得到ADB=90°,根据等腰三角形的性质得到∠ADO=∠A,∠BDO=∠ABD;得到∠PDO=90°,且D在圆上,于是得到结论;(2)连结OM,过D作DF⊥AB于F;由点M是 ![]() 的中点,得到OM⊥AB;设BD=x,根据已知条件得到AD=4x;由勾股定理得到AB=
的中点,得到OM⊥AB;设BD=x,根据已知条件得到AD=4x;由勾股定理得到AB= ![]() =
= ![]() x;根据三角形的面积公式解方程得到DF=
x;根据三角形的面积公式解方程得到DF= ![]() x,根据相似三角形的性质即可得到结论.
x,根据相似三角形的性质即可得到结论.
【考点精析】本题主要考查了相似三角形的判定与性质和解直角三角形的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.





