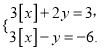��Ŀ����
����Ŀ��У����ȫ�ǽ���������ע���ش����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ��ѧ�С����������¼�·����ʻ�������ٶȵ�ʵ�飺���ڹ�·�Ա�ѡȡһ��C�����ڱ�ֱ�ij���L��ȷ����D��ʹCD��L��ֱ�����CD�ij�����24�ף���L�ϵ�D��ͬ��ȡ��A��B��ʹ��CAD=30�㣬��CBD=60�㣮 
��1����AB�ij�������������ţ���
��2����֪��·�ζ�У������Ϊ45ǧ��/Сʱ�������ij��У����A��B��ʱ2�룬����У���Ƿ��٣�˵�����ɣ����ο����ݣ� ![]() ��1.73��
��1.73�� ![]() ��1.41��
��1.41��
���𰸡�
��1���⣺���}��ã�
��Rt��ADC��AD= ![]() =
= ![]() =24
=24 ![]() ��36.33���ף���
��36.33���ף���
��Rt��BDC��BD= ![]() =
= ![]() =8
=8 ![]() ��
��
��AB=AD��BD=16 ![]() ��
��
��2���⣺���٣�
���ɣ���������A��B��ʱ2�룬
���ٶ�Ϊ16��1.73��2=13.84��/��
13.84��3.6=49.824ǧ��/ʱ��45ǧ��/Сʱ��
���У����AB·�γ��٣�
����������1���ֱ���Rt��ADC��Rt��BDC�У��������к������������AD��BD�ij����̶����AB�ij�����2���ɴ�A��B��ʱ2�룬�����������У�����ٶȣ��Ƚ���40ǧ��/Сʱ�Ĵ�С������ȷ������У���Ƿ��٣�

����Ŀ����������![]() ��ͼ��.
��ͼ��.
��1������![]() ���Ա���x��ȡֵ��Χ��________��
���Ա���x��ȡֵ��Χ��________��
��2���б����ѱ���������
x | ���� | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ���� |
y |
��3����㡢����
��4�����ͼ��д��������һ������________________________________________.