Question

【题目】已知：如图，在菱形ABCD中，AB=5，联结BD，sin∠ABD= ．点P是射线BC上的一个动点（点P不与点B重合），联结AP，与对角线BD相交于点E，联结EC．

（1）求证：AE=CE；
（2）当点P在线段BC上时，设BP=x，△PEC的面积为y，求y关于x的函数解析式，并写出它的定义域；
（3）当点P在线段BC的延长线上时，若△PEC是直角三角形，求线段BP的长．

Answer 1

【答案】
（1）

解：∵四边形ABCD是菱形，

∴BA=BC，∠ABE=∠CBE．

在△ABE和△CBE中，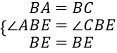

又∵BE=BE，

∴△ABE≌△CBE

∴AE=CE．

（2）

解：连接AC，交BD于点O，过点A作AH⊥BC，过点E作EF⊥BC，如图1所示：

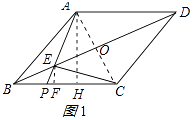
垂足分别为点H、F．

∵四边形ABCD是菱形，

∴AC⊥BD．

∵AB=5， ，

∴AO=OC= ，BO=OD= ．

∵ ，

∴AH=4，BH=3．

∵AD∥BC，

∴ ，

∴ ，

∴ ，

∴ ．

∵EF∥AH，

∴ ，

∴ ．

∴

（3）

解：因为点P在线段BC的延长线上，所以∠EPC不可能为直角．如图2所示：

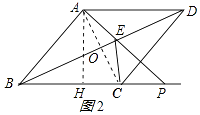
①当∠ECP=90°时

∵△ABE≌△CBE，

∴∠BAE=∠BCE=90°，

∵ ，

∴ ，∴BP= ．

②当∠CEP=90°时，

∵△ABE≌△CBE，

∴∠AEB=∠CEB=45°，

∴ ，

∴ ， ．

∵AD∥BP，

∴ ，

∴ ，

∴BP=15．

综上所述，当△EPC是直角三角形时，线段BP的长为 或15

【解析】（1）由菱形的性质得出BA=BC，∠ABD=∠CBD．由SAS证明△ABE≌△CBE，即可得出结论．（2）联结AC，交BD于点O，过点A作AH⊥BC于H，过点E作EF⊥BC于F，由菱形的性质得出AC⊥BD．由三角函数求出AO=OC= ，BO=OD= ．由菱形面积得出AH=4，BH=3．由相似三角形的性质得出 ，求出EF的长，即可得出答案；∴ ，（3）因为点P在线段BC的延长线上，所以∠EPC不可能为直角．分情况讨论：①当∠ECP=90°时，②当∠CEP=90°时，由全等三角形的性质和相似三角形的性质即可得出答案．
【考点精析】本题主要考查了菱形的性质的相关知识点，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能正确解答此题．