题目内容
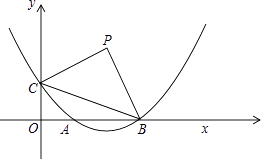
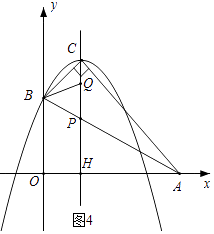
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x﹣c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.
【答案】
(1)
解:点B(0,2)向上平移6个单位得到点B'(0,8),
将A(4,0),B'(0,8)分别代入y=ax2+2x﹣c,得
![]() ,
,
解得 ![]() ,
,
∴原抛物线为y=﹣x2+2x+8,向下平移6个单位后所得的新抛物线为y=﹣x2+2x+2,
∴顶点C的坐标为(1,3)
(2)
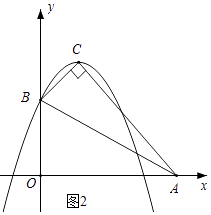
解:如图2,由A(4,0),B(0,2),C(1,3),得
AB2=20,AC2=18,BC2=2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴tan∠CAB= ![]() =
= ![]() =
= ![]() ;
;
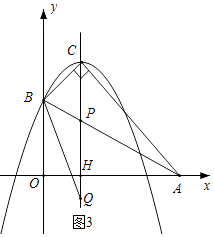
(3)
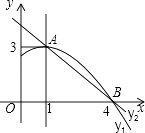
解:如图3,设抛物线的对称轴x=1与x轴交于点H,
由 ![]() =
= ![]() =
= ![]() ,得PH=
,得PH= ![]() AH=
AH= ![]() ,
,
∴P(1, ![]() ),
),
由HA=HC=3,得∠HCA=45°,
∴当点Q在点C下方时,∠BCQ=∠ACP,
因此△BCQ与△ACP相似分两种情况:
①如图3,当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,
,
解得CQ=4,
此时Q(1,﹣1);
②如图4,当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,
,
解得CQ= ![]() ,
,
此时Q(1, ![]() ).
).
【解析】(1)先根据点B(0,2)向上平移6个单位得到点B'(0,8),将A(4,0),B'(0,8)分别代入y=ax2+2x﹣c,得原抛物线为y=﹣x2+2x+8,向下平移6个单位后所得的新抛物线为y=﹣x2+2x+2,据此求得顶点C的坐标;(2)根据A(4,0),B(0,2),C(1,3),得到AB2=20,AC2=18,BC2=2,进而得出AB2=AC2+BC2 , 根据∠ACB=90°,求得tan∠CAB的值即可;(3)先设抛物线的对称轴x=1与x轴交于点H,根据 ![]() =
= ![]() =
= ![]() ,求得PH=
,求得PH= ![]() AH=
AH= ![]() ,进而得到P(1,
,进而得到P(1, ![]() ),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
【考点精析】利用二次函数的概念和二次函数的图象对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.

 阅读快车系列答案
阅读快车系列答案