Question

【题目】如图，一次函数的图象与反比例函数的图象交于点，与交于点，与轴交于点，轴于点，且．

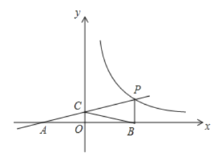
（1）求一次函数、反比例函数的解析式；

（2）根据图像直接写出的的取值范围；

（3）点为反比例函数图象上使得四边形为菱形的一点，点为轴上的一动点，当最大时，求点的坐标．

Answer 1

【答案】（1）yx+1，y；（2）0＜x＜4；（3）E(0，3)

【解析】

（1）先根据题意得出P点坐标，再将A、P两点的坐标代入y=kx+b求出kb的值，故可得出一次函数的解析式，把点P（4，2）代入反比例函数即可得出m的值，进而得出结论；
（2）利用图象法，写出反比例函数图象想一次函数图象的上方的自变量的取值范围即可；
（3）根据题意确定点P、点D坐标,求直线PD解析式，求其于y轴交点即为点E．

解：（1）∵AC＝BC，CO⊥AB，A（﹣4，0），

∴O为AB的中点，即OA＝OB＝4，

∴P（4，2），B（4，0），

将A（﹣4，0）与P（4，2）代入y＝kx+b得：

，解得：，

∴一次函数解析式为yx+1，

将P（4，2）代入反比例解析式得：m＝8，即反比例解析式为y

（2）观察图象可知，kx+b时，x的取值范围0＜x＜4．

（3）如图所示，

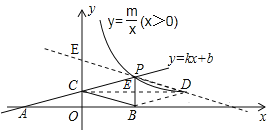
∵点C（0，1），B（4，0）

∴BC，PC，

∴以BC、PC为边构造菱形，

∵四边形BCPD为菱形，

∴PB垂直且平分CD，

∵PB⊥x轴，P（4，2），

∴点D（8，1）．

连接PD交y轴于点E，点E即为所求

设

将D（8，1），P（4，2）代入得： 解得：

∴

令，则

∴E（0,3）