题目内容

【题目】如我们把函数沿轴翻折得到函数，函数与函数的图象合起来组成函数的图象．若直线与函数的图象刚好有两个交点，则满足条件的的值可以为_______________(填出一个合理的值即可)．

【答案】（答案不唯一，满足k的取值范围即可）

【解析】

根据题意，画出图象，求出函数，根据题意和图象可知直线与y1和y2各有一个交点，然后联立方程求出交点的横坐标，再根据x的取值范围即可求出结论．

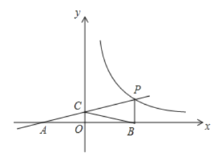
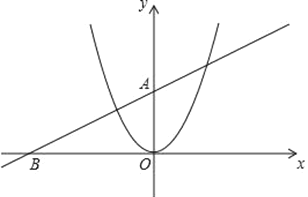
解：根据题意，画出如下图形

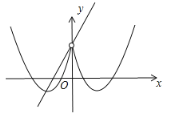
函数沿轴翻折得到函数解析式为

由图可知：若直线与函数的图象刚好有两个交点，

则直线与y1和y2各有一个交点

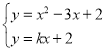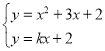联立①和②

解①，得x1=k＋3，x2=0（不符合取值范围，舍去）；解②，得x3=k－3，x4=0（不符合取值范围，舍去）

①中，x＞0，即k＋3＞0，②中，x＜0，即k－3＜0

∴-3＜k＜3

∴满足条件的的值可以为（答案不唯一，满足k的取值范围即可）．

故答案为：（答案不唯一，满足k的取值范围即可）．

练习册系列答案
相关题目

【题目】如图，一次函数的图象与反比例函数的图象交于点，与交于点，与轴交于点，轴于点，且．

（1）求一次函数、反比例函数的解析式；

（2）根据图像直接写出的的取值范围；

（3）点为反比例函数图象上使得四边形为菱形的一点，点为轴上的一动点，当最大时，求点的坐标．

【题目】如图，中，，点、同时从点出发，以的速度分别沿、匀速运动，当点到达点时，两点同时停止运动，设运动时间为．过点作的垂线交于点，点与点关于直线对称．

（1）当_____时，点在的平分线上；

（2）当_____时，点在边上；

（3）设与重合部分的面积为，求与之间的函数关系式，并写的取值范围．

【题目】已知直线y＝kx+b经过点A（0，2），B（﹣4，0）和抛物线y＝x2．

（1）求直线的解析式；

（2）将抛物线y＝x2沿着x轴向右平移，平移后的抛物线对称轴左侧部分与y轴交于点C，对称轴右侧部分抛物线与直线y＝kx+b交于点D，连接CD，当CD∥x轴时，求平移后得到的抛物线的解析式；

（3）在（2）的条件下，平移后得到的抛物线的对称轴与x轴交于点E，P为该抛物线上一动点，过点P作抛物线对称轴的垂线，垂足为Q，是否存在这样的点P，使以点E，P，Q为顶点的三角形与△AOB相似？若存在，请求出点P的坐标；若不存在，请说明理由．

【题目】如图，矩形纸片，是的中点，是上一动点，沿折叠，点落在点处；延长交于点，连接.

（1）求证：≌；

（2）当时，将沿折叠，点落在线段上点处.

①求证：∽；

②如果，，求的长.

【题目】如图，直线y＝x与反比例函数y＝（x＞0）的图象相交于点D，点A为直线y＝x上一点，过点A作AC⊥x轴于点C，交反比例函数y＝（x＞0）的图象于点B，连接BD．

（1）若点B的坐标为（8，2），则k＝　 　，点D的坐标为　 　；

（2）若AB＝2BC，且△OAC的面积为18，求k的值及△ABD的面积．

【题目】已知：在中，以边为直径的交于点，在劣弧上取一点使，延长依次交于点，交于．

（1）求证：；

（2）若，的直径等于10，，求的长．

【题目】已知甲、乙两地相距车和车分别从甲地和乙地同时出发，相向而行，沿同一 条公路驶往乙地和甲地后，车因临时需要，返回到这条公路上的丙地取物，然后又立即赶往乙地，结果比车晚到达目的地．两车的速度始终保持不变，如图是两车距各自出 发地的路程(单位：)，(单位：)与 车出发时间(单位:)的函数图象，请结合图象信息解答下列问题：

（1）A车的速度为 车的速度为

（2）求甲、丙两地的距离；

（3）求车出发多长时间，两车相距

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网