题目内容
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】分析:(1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,交B′C′于F.由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;
(2)设运动的时间为t秒,根据题意得:CC′=2t,DD′=t,则C′D′=CD+DD′-CC′=4+t-2t=4-t,由第(1)的结论列式得出结果;
(3)求出相切的时间,进而得出B点移动的距离.
详解:(1)假设第一次相切时,△ABC移至△A′B′C′处,
如图1,A′C′与⊙O切于点E,连接OE并延长,交B′C′于F,
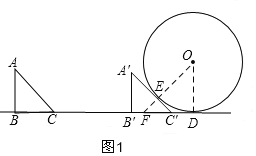
设⊙O与直线l切于点D,连接OD,则OE⊥A′C′,OD⊥直线l,
由切线长定理可知C′E=C′D,
设C′D=x,则C′E=x,
∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∴∠A′C′B′=∠ACB=45°,
∴△EFC′是等腰直角三角形,
∴C′F=![]() x,∠OFD=45°,
x,∠OFD=45°,
∴△OFD也是等腰直角三角形,
∴OD=DF,
∴![]() x+x=1,则x=
x+x=1,则x=![]() -1,
-1,
∴CC′=BD-BC-C′D=5-1-(![]() -1)=5-
-1)=5-![]() ,
,
∴点C运动的时间为![]() ;
;
则经过![]() 秒,△ABC的边与圆第一次相切;
秒,△ABC的边与圆第一次相切;
(2)如图2,设经过t秒△ABC的边与圆第一次相切,△ABC移至△A′B′C′处,⊙O与BC所在直线的切点D移至D′处,
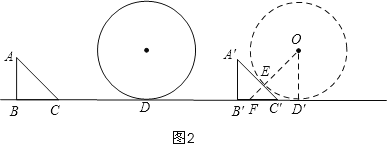
A′C′与⊙O切于点E,连OE并延长,交B′C′于F,
∵CC′=2t,DD′=t,
∴C′D′=CD+DD′-CC′=4+t-2t=4-t,
由切线长定理得C′E=C′D′=4-t,
由(1)得:4-t=![]() -1,
-1,
解得:t=5-![]() ,
,
答:经过5-![]() 秒△ABC的边与圆第一次相切;
秒△ABC的边与圆第一次相切;
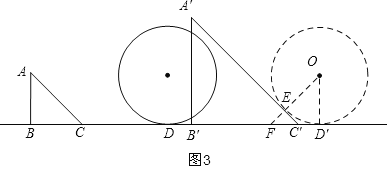
(3)由(2)得CC′=(2+0.5)t=2.5t,DD′=t,
则C′D′=CD+DD′-CC′=4+t-2.5t=4-1.5t,
由切线长定理得C′E=C′D′=4-1.5t,
由(1)得:4-1.5t=![]() -1,
-1,
解得:t=![]() ,
,
∴点B运动的距离为2×![]() =
=![]() .
.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】某旅行社一则旅游消息如下:
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加一人,人均收费减少 |
(![]() )甲公司员工分两批参加该项旅游,分别支付给旅行社
)甲公司员工分两批参加该项旅游,分别支付给旅行社![]() 元和
元和![]() 元,甲公司员工有__________人.
元,甲公司员工有__________人.
(![]() )乙公司员工一起参加该项旅游,支付给旅行社
)乙公司员工一起参加该项旅游,支付给旅行社![]() 元,乙公司员工多少人?
元,乙公司员工多少人?




