Question

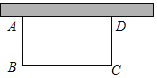
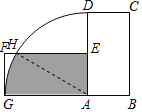
【题目】如图，将矩形ABCD绕点A逆时针旋转90°至矩形AEFG，点D的旋转路径为，若AB＝2，BC＝4，则阴影部分的面积为（　　）

A.B.C.D.

Answer 1

【答案】D

【解析】

设与EF交于H，连接AH，根据旋转的性质及矩形的性质得到AH＝AD＝BC＝4，又AE=AB=2，在Rt△AEH中，根据含30°角的直角三角形的性质定理的逆定理可得到∠AHE＝30°，再根据平行线的性质可得出∠GAH的度数，根据三角形和扇形的面积公式即可得到结论．

解：如图，设与EF交于H，连接AH，

∵四边形ABCD是矩形，AB＝2，BC＝4，

∴AH＝AD＝BC＝4，

∴∠AHE＝30°，

又四边形AEFG为矩形，∴EF∥AG,

∴∠GAH=∠AHE=30°，

∵AE＝AB＝2，

∴HE＝2，

∴阴影部分的面积＝S扇形AHG+S△AHE＝×2×2＝+2，

故选：D．