题目内容
【题目】小明研究一函数的性质,下表是该函数的几组对应值:
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
![]() 根据所画函数图象,写出该函数的一条性质: ;
根据所画函数图象,写出该函数的一条性质: ;
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是
的范围是

【答案】(1)详见解析;(2)![]() 时,
时,![]() 随
随![]() 的增大而减小(答案不唯一);(3)
的增大而减小(答案不唯一);(3) ;(4)
;(4)![]()
【解析】
(1)根据表格的点即可以画出图象;
(2)根据所画的图象即可写出性质;
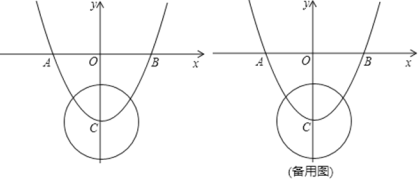
(3)通过表格的数据和所画的图象,可知,当x<1为二次函数,x≥1时为一次函数,故可设相应的解析式根据表格的点即可求出解析式及取值范围;
(4)可从图象看到两个临界点,一个是点(1,3),则可先求一次函数y=![]() x+n与直线交点求出n值,另一个则是与二次函数有且仅有一个交点时,即△=0时,即可以求出n值,要使一次函数y=
x+n与直线交点求出n值,另一个则是与二次函数有且仅有一个交点时,即△=0时,即可以求出n值,要使一次函数y=![]() x+n与该函数图象有三个交点,只要保证在两临界点对应的n值之间即可求.
x+n与该函数图象有三个交点,只要保证在两临界点对应的n值之间即可求.
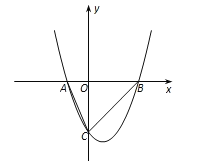
![]() 根据表格的点所画的图象如图所示:
根据表格的点所画的图象如图所示:
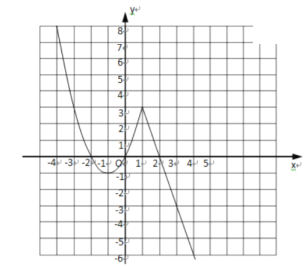
![]() 观察图象可得其中的一条性质为:x<1时,y随x的增大而减小
观察图象可得其中的一条性质为:x<1时,y随x的增大而减小
故答案为:x<1时,y随x的增大而减小;
(3)当x<1时,函数经过点点(3,3)(2,0)(0,0)
故设函数的解析式为y=a(x+2)(x0),
将点(4,6)代入解得3=a(3+2)×(3),解得a=1,
∴x<1时,函数解析式为:y=x2+2x,(x<1)
当x≥1时,函数经过点(1,3)(2,0)
故设函数解析式为:y=kx+b
代入得![]() ,解得
,解得![]()
∴x≥1时,函数解析式为:y=3x+6
故答案为: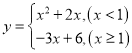 ;
;
(4)由图象可知,一次函数y=![]() x+n与函数y=3x+6交点在(1,3)时
x+n与函数y=3x+6交点在(1,3)时
有3=![]() +n得,n=
+n得,n=![]()
一次函数y=![]() x+n与y=x2+2x有且仅有一个交点时,有
x+n与y=x2+2x有且仅有一个交点时,有![]() x+n=x2+2x
x+n=x2+2x
化简得x2+![]() xn=0
xn=0
∴△=(![]() )24n=0,解得n=
)24n=0,解得n=![]()
故一次函数y=![]() x+n与该函数图象有三个交点时,n的范围是
x+n与该函数图象有三个交点时,n的范围是![]()
故答案为:![]() .
.