题目内容
【题目】如图,已知二次函数![]() 的图象与x轴交于A,B两点与y轴交于点C,⊙C的半径为
的图象与x轴交于A,B两点与y轴交于点C,⊙C的半径为![]() ,P为⊙C上一动点.
,P为⊙C上一动点.
(1)点B,C的坐标分别为B( ),C( );
(2)当P点运动到(-1,-2)时,判断PB与⊙C的位置关系,并说出理由;
(3)是否存在点P,使得△PBC是以BC为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(4)连接PB,若E为PB的中点,连接OE,则OE的最大值= .
【答案】(1)B(3,0),C(0,-4);(2)相切,理由详见解析;(3)存在,P1(-1,-2)或P2(![]() ,
,![]() );(4)
);(4)![]()
【解析】
(1)在抛物线中令y=0即可求出点B的坐标,令x=0即可求出点C的坐标;
(2)分别求出三边的长度即可得出答案;
(3)根据勾股定理求出BC和![]() 的长度,过
的长度,过![]() 作
作![]() ⊥x轴于点E,
⊥x轴于点E,![]() ⊥y轴于点F,根据相似三角形的性质得出
⊥y轴于点F,根据相似三角形的性质得出![]() ,设
,设![]() ,
,![]() 即可得出BE和CF的长度,解出x的值即可得出P2的坐标,同理即可得出P1的坐标;
即可得出BE和CF的长度,解出x的值即可得出P2的坐标,同理即可得出P1的坐标;
(4)根据中位线定理AP最大时,OE的值最大.
解:(1)在![]() 中,令 y=0, 则x=3 或-3,令 x=0, 则y=-4
中,令 y=0, 则x=3 或-3,令 x=0, 则y=-4
故B(3,0),C(0,-4);
(2)当P点运动到(-1,-2)时,PB与⊙C相切;
此时PB2=20,PC2=5,BC2=25,可得PB2+PC2=BC2,
从而CP⊥PB,∴PB与⊙C相切.
(3)存在点P,使得△PBC为直角三角形.
①当PB与圆O相切时,△PBC是直角三角形,如图,连接BC
∵OB=3,OC=4
∴BC=5
∵![]() ,
,![]()
∴![]()
过![]() 作
作![]() ⊥x轴于点E,
⊥x轴于点E,![]() ⊥y轴于点F
⊥y轴于点F
则△![]() ∽△
∽△![]() ,四边形
,四边形![]() 是矩形
是矩形
∴![]()
设![]() ,
,![]()
∴BE=3-x,CF=2x-4
∴![]()
解得:![]()
∴![]() ,
,![]()
∴P2(![]() ,
,![]() )
)
②同理求得:P1(-1,-2)
综上所述,点P的坐标为:P1(-1,-2)或P2(![]() ,
,![]() );
);
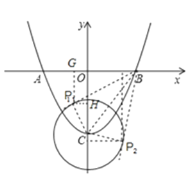
(4)![]()
如图∵E为PB的中点,OE是△BAP的中位线
∴OE=![]() AP
AP
∵![]()
∴![]()

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】小明研究一函数的性质,下表是该函数的几组对应值:
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
![]() 根据所画函数图象,写出该函数的一条性质: ;
根据所画函数图象,写出该函数的一条性质: ;
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是
的范围是