题目内容
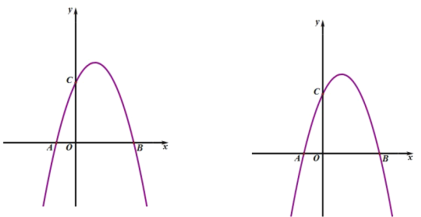
【题目】如图,已知二次函数y=x2-mx-m-1的图像交x轴于A、B两点(A、B分别位于坐标原点O的左、右两侧),交y轴于点C,且△ABC的面积为6.
(1)求这个二次函数的表达式;
(2)若P为平面内一点,且PB=3PA,试求当△PAB的面积取得最大值时点P的坐标,并求此时直线PO将△ABC分成的两部分的面积之比.
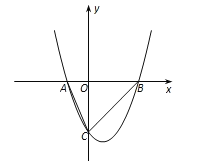
【答案】(1)y=x2-2x-3;(2)5∶3或1∶15.
【解析】
(1)分别求出A,B,C的坐标,结合△ABC的面积为6,列出关于m的方程,求出m的值,即可得到二次函数解析式;
(2)设P(a,b),根据PB=3PA以及两点间的距离公式,得到b2关于a的二次函数,利用二次函数的性质,求出使△PAB面积最大时,点P的坐标,然后分两种情况:①当P1(-![]() ,
,![]() )时,②当P2(-
)时,②当P2(-![]() ,-
,-![]() )时,分别求出此时直线PO将△ABC分成的两部分的面积之比,即可.
)时,分别求出此时直线PO将△ABC分成的两部分的面积之比,即可.
(1)令y=0,得:0=x2-mx-m-1,解得:x1=-1,x2=m+1,
∴A(-1,0),B(m+1,0).
当x=0时,y=-m-1,
∴C(0,-m-1).
∵B(m+1,0)在y轴的右侧,
∴m+1>0,
由“△ABC的面积为6”得:S=![]() (m+1)(m+2)=6,
(m+1)(m+2)=6,
解得:m1=-5(舍去),m2=2,
∴y=x2-2x-3.
(2)设P(a,b),
∵A(-1,0),B(3,0),PB=3PA,
∴PB2=9PA2,即(3-a)2+b2=9[(-1-a)2+b2],
化简得:b2=-a2-3a.
要使△PAB面积最大,底AB=4为定值,因此只要使AB边上的高最大,即b2取得最大值.
∵b2=-(a+![]() )2+
)2+![]() ,
,
∴当a=-![]() 时,b2取得最大值为
时,b2取得最大值为![]() ,即
,即![]() 取得最大值为
取得最大值为![]() ,
,
∴P1(-![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
①当P1(-![]() ,
,![]() )时,直线P1O的解析式为:y=-x,
)时,直线P1O的解析式为:y=-x,
∵B(3,0),C(0,-3),
∴直线BC的解析式为:y=x-3.
联立y=-x与y=x-3,得-x=x-3,解得:x=![]() ,
,
∴P1O与BC的交点Q1(![]() ,-
,-![]() ),
),
∴△OBQ1的面积=![]() ×3×
×3×![]() =
=![]() ,四边形ACQ1O的面积=6-
,四边形ACQ1O的面积=6-![]() =
=![]() ,
,
∴此时直线PO将△ABC分成的两部分的面积之比为![]() ∶
∶![]() ,即5∶3.
,即5∶3.
②当P2(-![]() ,-
,-![]() )时,与①同理可得直线PO将△ABC分成的两部分的面积之比为1∶15.
)时,与①同理可得直线PO将△ABC分成的两部分的面积之比为1∶15.

【题目】小明研究一函数的性质,下表是该函数的几组对应值:
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
![]() 根据所画函数图象,写出该函数的一条性质: ;
根据所画函数图象,写出该函数的一条性质: ;
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是
的范围是