Question

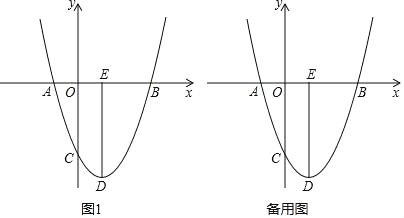
【题目】如图1，抛物线y＝ax2+bx﹣3经过点A，B，C，已知点A（﹣1，0），点B（3，0）

（1）求抛物线的解析式

（2）点D为抛物线的顶点，DE⊥x轴于点E，点N是线段DE上一动点

①当点N在何处时，△CAN的周长最小？

②若点M（m，0）是x轴上一个动点，且∠MNC＝90°，求m的取值范围．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）①N（1，﹣2）；②﹣≤m≤5．

【解析】

（1）函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），即可求解；

（2）①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小，即可求解；

②如图2，ME=﹣n2+3n，求出ME最大值，则可求出m的最小值；当点N与点D处时，m取得最大值，求解即可．

（1）函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），故﹣3a=﹣3，解得：a=1，故函数的表达式为：y=x2﹣2x﹣3；

（2）①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小．

设过点A、C'的一次函数表达式为y=kx+b，则：，解得：，故直线AC'的表达式为：y=﹣x﹣1，当x=1时，y=﹣2，故点N（1，﹣2）；

②如图2，过点C作CG⊥ED于点G．

设NG=n，则NE=3﹣n．

∵∠CNG+∠GCN=90°，∠CNG+∠MNE=90°，∴∠NCG=∠MNE，则tan∠NCG=n=tan∠MNE，故ME=﹣n2+3n，∴﹣1＜0，故ME有最大值，当n时，ME，则m的最小值为：；

如下图所示，当点N与点D重合时，m取得最大值．

过C作CG⊥ED于G．

∵y=x2﹣2x﹣3= y=（x－1）2﹣4，∴D（1，－4），∴CG=OE=1．

∵EG=OC=3∴GD=4－3=1，∴CG=DG=1，∴∠CDG=45°．

∵∠CDM=90°，∴∠EDM=45°，∴△EDM是等腰直角三角形，∴EM=ED=4，∴OM=OE+EM=1+4=5，∴m=5．

故：m≤5．