Question

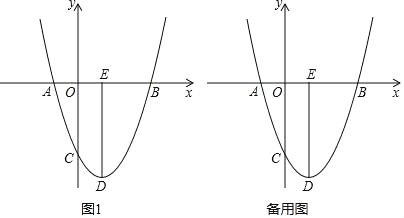
【题目】已知抛物线y=x+bx+c，经过点A（0，5）和点B（3，2）

（1）求抛物线的解析式：

（2）现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由；

（3）若⊙Q的半径为r，点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值

Answer 1

【答案】（1）

（2） P（2,1）或（1,2）或（-1,10）

（3）

【解析】

解：（1）将、代入方程中

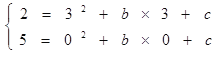
解得：

抛物线的解析式为：

（2）

抛物线的顶点是，和y轴的交点是

⊙P上一点和坐标轴相切就意味着抛物线上的点到坐标轴的距离是⊙P的半径1

即：抛物线上某点的横坐标或纵坐标为

当时，

当时，

当时，

当时，方程无解

存在⊙P与坐标轴相切的情况，且相切时圆点的坐标为、或

（3）⊙Q的点Q 在抛物线上，说明⊙Q的横纵坐标符合抛物线的方程

由第二问的说明得：⊙Q与两坐轴都相切，说明⊙Q的横纵坐标的绝对值相等，有因为Q的特点，纵坐标恒为正，则有带入抛物线的方程：