题目内容
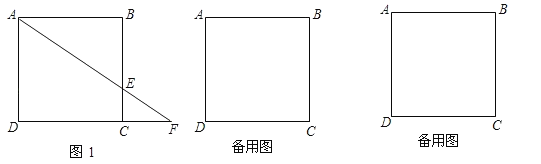
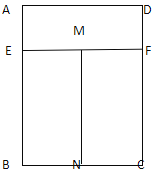
【题目】如图，矩形窗户边框ABCD由矩形AEFD，矩形BNME，矩形CFMN组成，其中AE：BE=1：3.已知制作一个窗户边框的材料的总长是6米，设BC=x(米)，窗户边框ABCD的面积为S(米2)
(1)①用x的代数式表示AB；
②求x的取值范围.
(2)求当S达到最大时，AB的长.
【答案】(1)①AB=
；②0＜x＜2；(2)x=1时S有最大值
，此时AB=米
【解析】
（1）①设AE=a，根据题意列式即可得到结论；②解不等式即可得到结论；
（2）根据题意求得函数的解析式S=ABBC=
，根据二次函数的性质即可得到结论．
解：（1）①∵BC=x，
∴AD=EF=BC=x，
∵AE：BE=1：3，
∴设AE=a，
∴AB=CD=4a，MN=BE=3a，
∴AB+CD+MN=11a，
∵制作一个窗户边框的材料的总长是6米，
∴11a+3x=6，
∴
，
∴AB=；
②∵AB＞0，BC＞0
∴＞0且x＞0
解得 ：0＜x＜2；
(2)S=AB×BC
=
=
+
∴当x=1时S有最大值，
此时AB=(米).
练习册系列答案
相关题目
【题目】抛物线y＝ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中正确的是（ ）
A. 抛物线与x轴的一个交点为（4，0）
B. 函数y＝ax2+bx+c的最大值为6
C. 抛物线的对称轴是x＝
D. 在对称轴右侧，y随x增大而增大
