题目内容
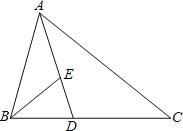
【题目】如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线。若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?( )
A. 1:6B. 1:9C. 2:13D. 2:15
【答案】D
【解析】
根据已知条件先求得S△ABE:S△BED=2:1,再根据三角形相似求得S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得答案.
S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得答案.
解:∵AE:ED=2:1,
∴S△ABE:S△BED=2:1,AE:AD=2:3,
∵∠ABE=∠C,∠BAE=∠CAD,
∴△ABE∽△ACD,
∴S△ABE:S△ACD=4:9,
∴S△ACD=![]() S△ABE,
S△ABE,
∵S△ABE=2S△BED,
∴S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,
S△BED,
∵S△ABC=S△ABE+S△ACD+S△BED=2S△BED+![]() S△BED+S△BED=
S△BED+S△BED=![]() S△BED,
S△BED,
∴S△BDE:S△ABC=2:15,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
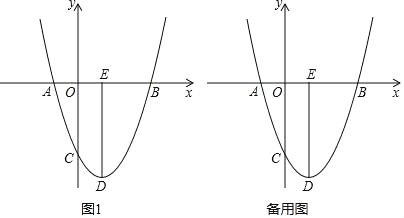
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是( )
A. 抛物线与x轴的一个交点为(4,0)
B. 函数y=ax2+bx+c的最大值为6
C. 抛物线的对称轴是x=![]()
D. 在对称轴右侧,y随x增大而增大