题目内容
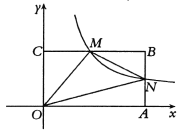
【题目】如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.

(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①当t=2时,线段PQ的最大值为
x+2;(2)①当t=2时,线段PQ的最大值为![]() ;②满足条件的P点坐标为(3,2)或(
;②满足条件的P点坐标为(3,2)或(![]() ,
,![]() ).
).
【解析】
(1)设交点式y=a(x+1)(x-4),再展开可得到-4a=2,解得a=-![]() ,然后写出抛物线解析式;
,然后写出抛物线解析式;
(2)①作PN⊥x轴于N,交BC于M,如图,先利用待定系数法求出直线BC的解析式为y=-![]() x+2,设P(t,﹣
x+2,设P(t,﹣![]() t2+
t2+![]() t+2),则M(t,-
t+2),则M(t,-![]() t+2),用t表示出PM=-
t+2),用t表示出PM=-![]() t2+2t,再证明△PQM∽△BOC,利用相似比得到PQ=﹣
t2+2t,再证明△PQM∽△BOC,利用相似比得到PQ=﹣![]() t2+
t2+![]() t,然后利用二次函数的性质解决问题;
t,然后利用二次函数的性质解决问题;
②讨论:当∠PCQ=∠OBC时,△PCQ∽△CBO,PC∥x轴,利用对称性可确定此时P点坐标;当∠CPQ=∠OBC时,△CPQ∽△CBO,则∠CPQ=∠MPQ,所以△PCM为等腰三角形,
则PC=PM,利用两点间的距离公式得到t2+(﹣![]() t2+
t2+![]() t+2﹣2)2=(﹣
t+2﹣2)2=(﹣![]() t2+2t)2,然后解方程求出t得到此时P点坐标.
t2+2t)2,然后解方程求出t得到此时P点坐标.
(1)抛物线解析式为y=a(x+1)(x﹣4),
即y=ax2﹣3ax﹣4a,
则﹣4a=2,解得a=﹣![]() ,
,
所以抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)①作PN⊥x轴于N,交BC于M,如图,
BC=![]() ,
,
当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
设直线BC的解析式为y=mx+n,
把C(0,2),B(4,0)得![]() ,解得
,解得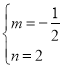 ,
,
∴直线BC的解析式为y=﹣![]() x+2,
x+2,
设P(t,﹣![]() t2+
t2+![]() t+2),则M(t,﹣
t+2),则M(t,﹣![]() t+2),
t+2),
∴PM=﹣![]() t2+
t2+![]() t+2﹣(﹣
t+2﹣(﹣![]() t+2)=﹣
t+2)=﹣![]() t2+2t,
t2+2t,
∵∠NBM=∠NPQ,
∴△PQM∽△BOC,
∴![]() ,即PQ=
,即PQ=![]() ,
,
∴PQ=﹣![]() t2+
t2+![]() t=﹣
t=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,
,
∴当t=2时,线段PQ的最大值为![]() ;
;
②当∠PCQ=∠OBC时,△PCQ∽△CBO,
此时PC∥OB,点P和点C关于直线x=![]() 对称,
对称,
∴此时P点坐标为(3,2);
当∠CPQ=∠OBC时,△CPQ∽△CBO,
∵∠OBC=∠NPQ,
∴∠CPQ=∠MPQ,
而PQ⊥CM,
∴△PCM为等腰三角形,
∴PC=PM,
∴t2+(﹣![]() t2+
t2+![]() t+2﹣2)2=(﹣
t+2﹣2)2=(﹣![]() t2+2t)2,
t2+2t)2,
解得t=![]() ,
,
此时P点坐标为(![]() ,
,![]() ),
),
综上所述,满足条件的P点坐标为(3,2)或(![]() ,
,![]() ).
).

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
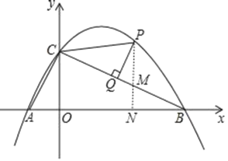
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?