��Ŀ����
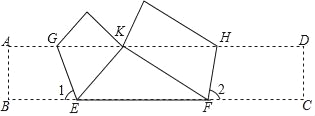
����Ŀ����14�֣���ͼ1����ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������B���߶�AE�ϣ���C���߶�AD�ϣ�
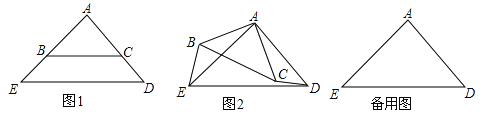
��1����ֱ��д���߶�BE���߶�CD�Ĺ�ϵ�� ��
��2����ͼ2����ͼ1�е���ABC�Ƶ�A˳ʱ����ת������0������360������
����1���еĽ����Ƿ��������������������ͼ2֤����������������˵�����ɣ�
����AC=![]() EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
���𰸡���1��BE=CD����2���������������ڣ���=45����
��������
���⣨1������ABC����AED���ǵ���ֱ�������Σ��õ�AB=AC��AE=AD�����ɵõ�BE=CD��
��2��������ABC����AED���ǵ���ֱ�������Σ��õ�AB=AC��AE=AD������ת�����ʿɵ���BAE=��CAD���õ���BAE�ա�CAD������ȫ�������ε����ʼ��ɵõ����ۣ�
����ƽ���ı��ε����ʿɵ���ABC=��ADC=45�������ɵ���ֱ�������ε����ʼ��ɵõ����ۣ�
�����������1���ߡ�ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������AB=AC��AE=AD����AE��AB=AD��AC����BE=CD��
��2�����������������£�
�ߡ�ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������AB=AC��AE=AD������ת�����ʿɵ���BAE=��CAD������BAE����CAD�У���AB=AC����BAE=��CAD��AE=AD�����BAE�ա�CAD��SAS������BE=CD��
�����ڣ���=45��������A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ����ABC=��ADC=45������AC=![]() ED�����CAD=45�����������Ķ�����45����
ED�����CAD=45�����������Ķ�����45����

 ���������ν�ϵ�д�
���������ν�ϵ�д�