题目内容
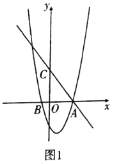
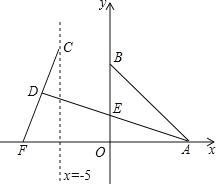
【题目】如图,已知A、B两点的坐标分别为(8,0),(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,则△ABE面积的最大值为_____.
【答案】![]()
【解析】
连接DK,由勾股定理得AD=12,再根据锐角三角函数得OE=![]() ,即可求出BE的长度,再根据三角形面积公式求解即可.
,即可求出BE的长度,再根据三角形面积公式求解即可.
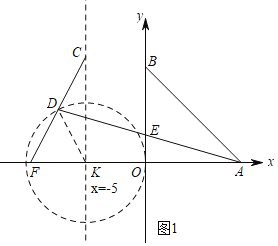
解:如图1,设直线x=﹣5交x轴于K.连接DK,
由题意KD=![]() CF=5,
CF=5,
∴点D的运动轨迹是以K为圆心,5为半径的圆,
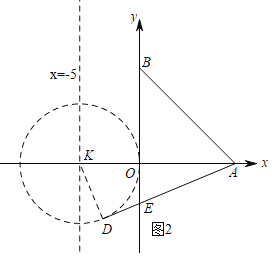
∴当直线AD与⊙K相切时,△ABE的面积最大,如图2,连接KD,
∵AD是切线,点D是切点,
∴AD⊥KD,
∵AK=5+8=13,DK=5,
∴AD=12,
∵tan∠EAO=![]() ,即
,即![]() ,
,
∴OE=![]() ,
,
∴BE=8+![]() =
=![]() ,
,
∴S△ABE=![]() BEOA=
BEOA=![]() =
=![]() .
.
故答案为:![]() .
.

【题目】某校为了解八年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() .
.![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
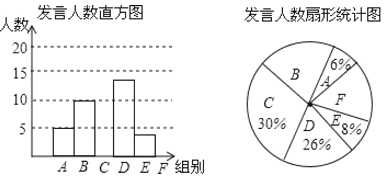
(1)求出样本容量,并补全直方图;
(2)该年级共有学生1500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知![]() 组发言的学生中恰有1位男生,
组发言的学生中恰有1位男生,![]() 组发言的学生中有2位女生.现从
组发言的学生中有2位女生.现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的![]() 型智能手表,去年销售总额为80000元,今年
型智能手表,去年销售总额为80000元,今年![]() 型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少
型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少![]() .
.
(1)求今年![]() 型智能手表每只售价多少元?
型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批![]() 型智能手表和
型智能手表和![]() 型智能手表共100只,它们的进货价与销售价格如下表所示,若
型智能手表共100只,它们的进货价与销售价格如下表所示,若![]() 型智能手表进货量不超过
型智能手表进货量不超过![]() 型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
|
| |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%
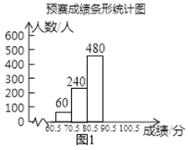
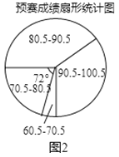
【题目】为了弘扬中华优秀传统文化,用好汉字,某中学开展了一次“古诗词”知识竞赛,赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分,统计成绩后绘制成如图1和图2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”(采用百分制记分,得分都为60分以上的整数).
前10名选手成绩统计表
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
预赛成绩(分) | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
复赛成绩(分) | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
总成绩(分) | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
(1)求该中学学生的总人数,并将图1补充完整;
(2)在图2中,求“90.5~100.5分数段人数”的圆心角度数;
(3)预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”,若按预赛成绩占40%,复赛成绩占60%的比例计算总成绩,并从中选出3人参加决赛,你认为选哪几号选手去参加决赛,并说明理由.