题目内容
【题目】如图,一次函数y=kx+1与反比例函数y=![]() 的图象相交于A(2,3),B两点.
的图象相交于A(2,3),B两点.
(1)求k、m的值和B点坐标;
(2)过点B作BC⊥x轴于C,连接AC,将△ABC沿x轴向右平移,对应得到△A'B'C',当反比例函数图象经过A'C'的中点M时,求△MAC的面积.
【答案】(1)m=6,k=1,点B的坐标为(﹣3,﹣2);(2)![]() .
.
【解析】
(1)将点A分别代入即可求出k与m的值,再将两个函数解析式联立成方程组即可求出点B的坐标;
(2)设△ABC向右平移了m个单位,将点点M(m﹣![]() ,
,![]() )代入y=
)代入y=![]() 中求出点M的坐标,过点A作y轴的平行线交CM于点H,利用直线CM求出点H,即可求出△MAC的面积.
中求出点M的坐标,过点A作y轴的平行线交CM于点H,利用直线CM求出点H,即可求出△MAC的面积.
解:(1)∵点A(2,3)在y=![]() 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为:y=![]() ①,
①,
将点A的坐标代入一次函数表达式得:3=2k+1,
解得:k=1,
故一次函数表达式为:y=x+1②,
联立①②得 ,解得:
,解得:![]() 或
或![]() ,
,
故点B的坐标为(﹣3,﹣2);
(2)如图,设△ABC向右平移了m个单位,则点A′、C′的坐标分别为(2+m,3)、(﹣3+m,0),
则点M(m﹣![]() ,
,![]() ),
),
将点M的坐标代入①式并解得:m=![]() ,
,
故点M(4,![]() ),
),
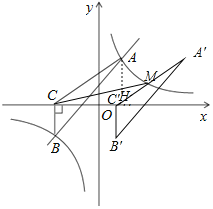
过点A作y轴的平行线交CM于点H,
设直线CM的解析式为y=k1x+b,
∴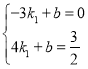 ,解得
,解得 ,
,
∴直线CM的表达式为:![]() ,
,
当x=2时,y=![]() ,故点H(2,
,故点H(2,![]() ),
),
△MAC的面积S=S△AHC+S△AHM=![]() ×AH×(xM﹣xC)=
×AH×(xM﹣xC)=![]() (3﹣
(3﹣![]() )×(4+3)=
)×(4+3)=![]() .
.

练习册系列答案
相关题目