题目内容
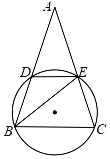
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 的切线
的切线![]() ,切点是
,切点是![]() ,过点
,过点![]() 作弦
作弦![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
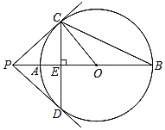
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)第一问考查切线的证明,总体思路为“连半径,证垂直”,根据题目已知PC是圆的切线,连接OD后,可根据![]() 利用垂径定理,结合角的互换或者证明△PCO与△PDO全等,进一步证明垂直即可解答。
利用垂径定理,结合角的互换或者证明△PCO与△PDO全等,进一步证明垂直即可解答。
(2)第二问根据AB是直径,可据此可知考查圆周角定理的运用,同时在直角三角形中要结合正切三角函数具体特点进行边的互换,具体可做辅助线结合勾股定理解答。
解(1)证明:连接![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,即
,即![]() ,
,
∵![]() ∴
∴![]()
∴![]()
∴![]()
∵![]() ∴
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
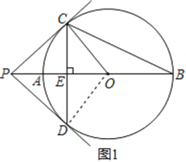
(2)如图2,连接![]() ,
,
∵![]() 是
是![]() 的直径,∴
的直径,∴![]() ,
,
∴![]()
设![]() ,
,![]() ,则由勾股定理得:
,则由勾股定理得:![]() ,解得:
,解得:![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]()
∵![]()
在![]() 中,
中,![]() ,
,
∵![]()
∴![]() ,即
,即![]() ,
,
∴![]()
∴![]()

练习册系列答案
相关题目
【题目】某班兴趣小组对函数y=﹣x2+2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣3 |
| 0 | 1 | 0 | 1 | 0 |
| ﹣3 | … |
(1)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分;
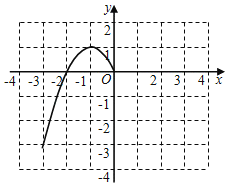
(2)观察函数图象,当y随x增大而减小时,则x的取值范围是
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程﹣x2+2|x|=0有 个实数根;
②方程﹣x2+2|x|=﹣1有 个实数根;
③若关于x的方程﹣x2+2|x|=n有4个实数根,则n的取值范围是 .