题目内容
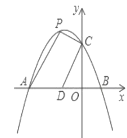
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴相交于点A(-1,0),B(4,0),与
轴相交于点A(-1,0),B(4,0),与![]() 轴相交于点C.
轴相交于点C.
(1)求该函数的表达式;
(2)若点P(2,m)为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC,求线段PQ的长;
(3)在(2)的条件下,点M为该函数图象上一点,且∠MAP=45°,求点M的坐标.
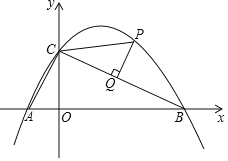

【答案】(1)![]() ;(2)
;(2)![]() ;(3)(4,0).
;(3)(4,0).
【解析】
(1)把点A、B代入二次函数的解析式,求出a、b的值,即可得到答案;
(2)作PN⊥x轴与N,交BC于点G,先求出点P和点C,然后得到直线BC的解析式,从而得到点N和点G的坐标,得到PG的长度,然后利用△PQG∽△BOC,即可求出PQ的长度;
(3)连接AP,则得到△APN是等腰直角三角形,则∠PAN=45°,则点M与点B重合,即可得到点M的坐标.
解:(1)根据题意,把点A、B代入抛物线![]() ,得
,得
![]() ,
,
解得: ,
,
∴二次函数的解析式为:![]() ;
;
(2)如图,作PN⊥x轴与N,交BC于点G,
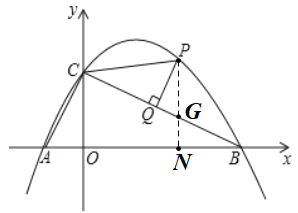
∵点P(2,m)在抛物线上,则
![]() ,
,
令x=0,则y=2,
∴点P为(2,3),点C为(0,2),点N为(2,0),
设直线BC为![]() ,则
,则
![]() ,解得:
,解得: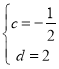 ,
,
∴直线BC的解析式为:![]() ;
;
令![]() ,
,![]() ,
,
∴点G的坐标为:(2,1),
∴PG=2,
∵OC∥PN,PQ⊥BC,
∴∠OCB=∠PGQ,∠BOC=∠PQG=90°,
∴△PQG∽△BOC,
∴![]() ,
,
∵BO=4,PG=2,![]() ,
,
∴![]() ;
;
(3)如图,连接AP,
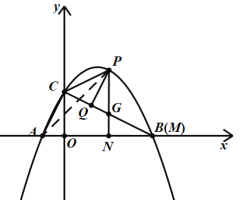
由(2)可知,点P为(2,3),点N为(2,0),点A为(-1,0),
∴AN=PN=3,
∵PN⊥AN,
∴△APN是等腰直角三角形,
∴∠PAN=45°,
∵点M在抛物线上,且∠MAP=45°,
∴点M与点B重合,此时点M的坐标为(4,0);
∴点M的坐标为:(4,0).

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】已知关于x的函数y=![]() +x,如表是y与x的几组对应值:
+x,如表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | -2 | - | -1 | - | - |
|
| 1 |
| 2 | 3 | 4 | … |
y | … | - | - | - | - | -2 | - | - |
|
| 2 |
|
|
|
| … |
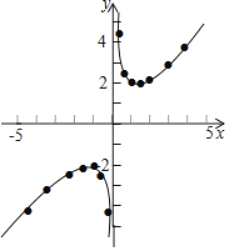
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出了此函数的图象请你根据学习函数的经验,根据画出的函数图象特征,对该函数的图象与性质进行探究:
(1)该函数的图象关于 对称;
(2)在y轴右侧,函数变化规律是当0<x<1,y随x的增大而减小;当x>1,y随x的增大而增大.在y轴左侧,函数变化规律是 .
(3)函数y=![]() 当x 时,y有最 值为 .
当x 时,y有最 值为 .
(4)若方程![]() +x=m有两个不相等的实数根,则m的取值范围是 .
+x=m有两个不相等的实数根,则m的取值范围是 .