题目内容
【题目】如图,点A,B,C在⊙O上,AB∥OC.
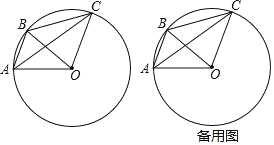
(1)求证:∠ACB+∠BOC=90°;
(2)若⊙O的半径为5,AC=8,求BC的长度.
【答案】(1)证明见解析;(2)BC=6.
【解析】
(1)根据圆周角定理求出∠AOB=2∠ACB,根据平行线的性质和等腰三角形的性质得出∠ABO=∠BAO,∠ABO=∠BOC,∠BAO+∠AOC=180°,即可得出答案;
(2)求出△BOC≌△DOC,根据全等三角形的性质得出BC=CD,根据勾股定理求出CD即可.
(1)证明:∵圆弧AB对的圆周角是∠ACB,对的圆心角是∠AOB,
∴∠AOB=2∠ACB,
∵OB=OA,
∴∠ABO=∠BAO,
∵AB∥OC,
∴∠ABO=∠BOC,∠BAO+∠AOC=180°,
∴∠BAO+∠AOB+∠BOC=180°,
即2∠ACB+2∠BOC=180°,
∴∠ACB+∠BOC=90°;
(2)延长AO交⊙O于D,连接CD,

则∠ACD=90°,
由勾股定理得:CD=![]() =
=![]() =6,
=6,
∵OC∥AB,
∴∠BOC=∠ABO,∠COD=∠BAO,
∵∠BAO=∠ABO,
∴∠BOC=∠COD,
在△BOC和△DOC中
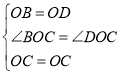
∴△BOC≌△DOC(SAS),
∴BC=CD,
∵CD=6,
∴BC=6.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目