题目内容
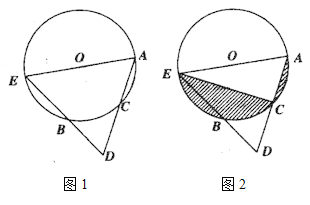
【题目】如图1,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接CE,⊙O的半径为5,AC长为4,求阴影部分面积之和.(保留![]() 与根号) .
与根号) .
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CB,AB,CE,由点C为劣弧AB上的中点,可得出CB=CA,再根据CD=CA,得△ABD为直角三角形,可得出∠ABE为直角,根据90度的圆周角所对的弦为直径,从而证出AE是⊙O的直径;
(2)由(1)得△ACE为直角三角形,根据勾股定理得出CE的长,阴影部分的面积等于半圆面积减去三角形ACE的面积.
(1)证明:连接CB,AB,CE,
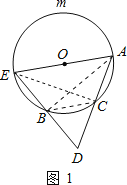
∵点C为劣弧AB上的中点,
∴CB=CA,
又∵CD=CA,
∴AC=CD=BC,
∴∠ABC=∠BAC,∠DBC=∠D,
∵Rt△斜边上的中线等于斜边的一半,
∴∠ABD=90°,
∴∠ABE=90°,
即弧AE的度数是180°,
∴AE是⊙O的直径;
(2)解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=10,AC=4,
∴根据勾股定理得:CE=2![]() ,
,
∴S阴影=S半圆-S△ACE=12.5π-![]() ×4×2
×4×2![]()
=![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的对应值如图,下列说法错误的是:( )
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是(0,4)
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而增大