题目内容
【题目】如图,在⊙O中,AB是直径,弦BE的垂直平分线交⊙O于点C,CD⊥AB于D,AD=1,BE=6,则BD的长为__.
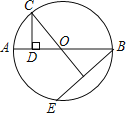
【答案】9.
【解析】
先证△BOF≌△COD,即可得CD=BF,根据垂径定理即可求出BF,从而求出CD,再根据勾股定理列方程即可求出圆的半径,从而求出BD.
弦BE的垂直平分线交BE于点F.

∴BF=![]() BE=3,∠BFO=90°,
BE=3,∠BFO=90°,
∵CD⊥AB,
∴∠ODC=∠BFO=90°,
∵OB=OC,∠BOF=∠COD,
∴△BOF≌△COD(AAS),
∴CD=BF=3,
设⊙O的半径为r,则OD=OA-AD=r﹣1,
由勾股定理得:OC2=OD2+CD2,
r2=(r﹣1)2+32,
r=5,
∴BD=AB﹣1=2×5﹣1=9,
故答案为:9.

练习册系列答案
相关题目
【题目】某小型工厂9月份生产的A、B两种产品数量分别为200件和100件,A、B两种产品出厂单价之比为2:1,由于订单的增加,工厂提高了A、B两种产品的生产数量和出厂单价,10月份A产品生产数量的增长率和A产品出厂单价的增长率相等,B产品生产数量的增长率是A产品生产数量的增长率的一半,B产品出厂单价的增长率是A产品出厂单价的增长率的2倍.设B产品生产数量的增长率为x(x>0).
(1)用含有x的代数式填表(不需化简):
9月份生产数量 | 生产数量的增长率 | 10月份生产数量 | |
产品A | 200 |
|
|
产品B | 100 | x |
|
(2)若9月份两种产品出厂单价的和为90元,10月份该工厂的总收入增加了4.4x,求x的值.