题目内容
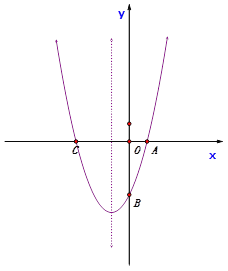
【题目】如图，已知抛物线
经过点A（1,0）和点B （0，-3），与x轴交于另一点C。
（1）求抛物线的解析式。
（2）在抛物线上是否存在一点D，使△ACD的面积与△ABC的面积相等（点D不与点B重合）？若存在，求出点D的坐标；若不存在，请说明理由。
（3）若点P是抛物线上的动点，点Q是抛物线对称轴上的动点，那么是否存在这样的点P，使以点A、C、P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由。
【答案】(1)抛物线的解析式为:
. (2)D（-2，-3）（-1±
，3）(3) P（-5，12）（3，12）（-1，-4）
【解析】
（1）由待定系数法，把点A、B代入解析式，求出a、b的值，即可得到答案；
（2）先求出点C的坐标，得到AC和OB的长度，计算出面积，根据面积相等，则设D点坐标为（x，y），求出y的值，然后代入二次函数解析式求出x，即可得到答案；
（3）根据题意，可分为AC为对角线和AC为边长，两种情况进行讨论，然后根据平行四边形的性质，即可求出P点坐标.
解：（1）把点A （1，0）和点B （0，-3）代入二次函数解析式，则
，解得：
，
∴抛物线的解析式为：.
（2）存在；
由（1）可知，二次函数的对称轴为：
，
∴点C坐标为：（-3，0），
∴AC=4，OB=3，
∴△ABC的面积为：
；
设点D坐标为（x，y），则
，
解得：
，
∴
.
当
时，有
，
解得：
，
∴点D为：（-1±，3）；
当
时，有
，
解得：
，
当
时为点B，舍去，
∴点D为（
）；
综合上述，点D的坐标为：（-1±，3）或（）；
（3）存在；
以点A、C、P、Q为顶点的四边形为平行四边形，则分为两种情况：
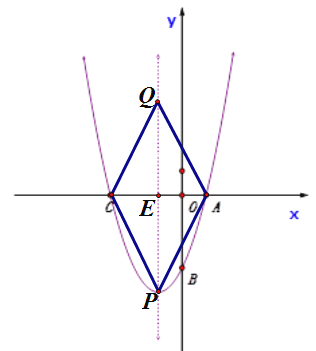
当AC为对角线时，如图：此时点P在对称轴上，且点P为抛物线的顶点；
当
时，代入抛物线解析式，得
，
则点P坐标为：（
）；
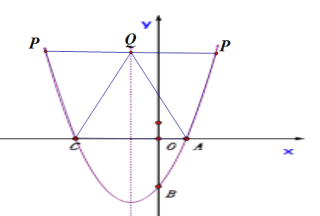
②当AC为边长时，如图，此时PQ∥AC，PQ=AC=4，
，
∵点Q在直线上，
∴点P的横坐标为：
或
，
当
时，有
，
∴点P为：（3，12）；
当
时，有
，
∴点P为：（-5，12）；
综合上述，点P的坐标为：（-5，12）或（3，12）或（-1，-4）.
