题目内容
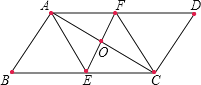
【题目】如图，正方形 ABCD 的边长为 8，E 是 BC 边的中点，点 P 在射线 AD 上， 过 P 作 PF⊥AE 于 F．
（1）请判断△PFA 与△ABE 是否相似，并说明理由；
（2）当点 P 在射线 AD 上运动时，设 PA＝x，是否存在实数 x，使以 P，F，E 为顶 点的三角形也与△ABE 相似？若存在，请求出 x 的值；若不存在，说明理由．
【答案】（1）见解析；（2）存在，x的值为2或5.
【解析】
（1）在△PFA与△ABE中，易得∠PAF=∠AEB及∠PFA=∠ABE=90°；故可得△PFA∽△ABE；
（2）根据题意：若△EFP∽△ABE，则∠PEF=∠EAB；必须有PE∥AB；分两种情况进而列出关系式．
(1)证明：∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°，
∴△PFA∽△ABE.
(2)
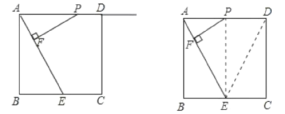
若△EFP∽△ABE，则∠PEF=∠EAB.
如图，连接PE,DE,
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2，即x=2.
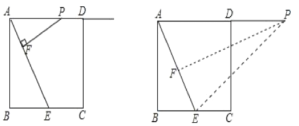
如图，延长AD至点P，作PF⊥AE于点F,连接PE,
若△PFE∽△ABE，则∠PEF=∠AEB.
∵∠PAF=∠AEB，
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE，
∴点F为AE的中点.
∵AE=
，
∴EF=
AE=
.
∵
，
∴PE=5，即x=5.
∴满足条件的x的值为2或5.
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
【题目】为了增强环境保护意识，在环保局工作人员指导下，若干名“环保小卫士” 组成了“控制噪声污染”课题学习研究小组．在“世界环境日”当天，该小组抽样 调查了全市 40 个噪声测量点在某时刻的噪声声级（单位：dB），将调查的数据进行
处理（设所测数据均为正整数），得频数分布表如下：
组别 | 噪声声级分组 | 频数 | 频率 |
1 | 44.5～59.5 | 4 | 0.1 |
2 | 59.5～74.5 | a | 0.2 |
3 | 74.5～89.5 | 10 | 0.25 |
4 | 89.5～104.5 | b | c |
5 | 104.5～119.5 | 6 | 0.15 |
合计 | 40 | 1.00 |
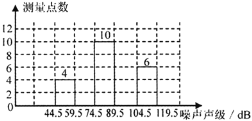
根据表中提供的信息解答下列问题：
（1）频数分布表中的a＝ ， b＝ ， c＝ ；
（2）补充完整频数分布直方图；
（3）如果全市共有 300 个测量点，那么在这一时刻噪声声级小于 75dB 的测量点约有多少个？
