题目内容
在平面直角坐标系xOy中,抛物线y=x2﹣(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,﹣1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.
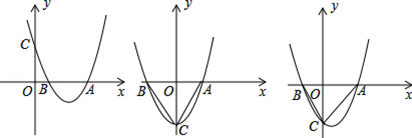
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,﹣1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.

(1)A(2,0),B(1,0);(2)∠ACB=90°;
(3)①当AC=BC时,n=﹣2;
②当AC=AB时,n=﹣ ;
;
③当BC=AB时,当n>0时,n= ,当n<0时,n=﹣
,当n<0时,n=﹣ .
.
(3)①当AC=BC时,n=﹣2;
②当AC=AB时,n=﹣
 ;
;③当BC=AB时,当n>0时,n=
 ,当n<0时,n=﹣
,当n<0时,n=﹣ .
.试题分析:
(1)已知m,n的值,即已知抛物线解析式,求解y=0时的解即可.此时y=x2﹣(m+n)x+mn=(x﹣m)(x﹣n),所以也可直接求出方程的解,再代入m,n的值,推荐此方式,因为后问用到的可能性比较大.
(2)求∠ACB,我们只能考虑讨论三角形ABC的形状来判断,所以利用条件易得﹣1=mn,进而可以用m来表示A、B点的坐标,又C已知,则易得AB、BC、AC边长.讨论即可.
(3)△ABC是等腰三角形,即有三种情形,AB=AC,AB=BC,AC=BC.由(2)我们可以用n表示出其三边长,则分别考虑列方程求解n即可.
试题解析:
解:(1)∵y=x2﹣(m+n)x+mn=(x﹣m)(x﹣n),
∴x=m或x=n时,y都为0,
∵m>n,且点A位于点B的右侧,
∴A(m,0),B(n,0).
∵m=2,n=1,
∴A(2,0),B(1,0).
(2)∵抛物线y=x2﹣(m+n)x+mn(m>n)过C(0,﹣1),
∴﹣1=mn,
∴n=﹣
 ,
,∵B(n,0),
∴B(﹣
 ,0).
,0).∵AO=m,BO=﹣
 ,CO=1
,CO=1∴AC=
 =
= ,
,BC=
 =
=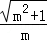 ,
,AB=AO+BO=m﹣
 ,
,∵(m﹣
 )2=(
)2=( )2+(
)2+(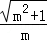 )2,
)2,∴AB2=AC2+BC2,
∴∠ACB=90°.
(3)∵A(m,0),B(n,0),C(0,mn),且m=2,
∴A(2,0),B(n,0),C(0,2n).
∴AO=2,BO=|n|,CO=|2n|,
∴AC=
 =
= ,
,BC=
 =
= |n|,
|n|,AB=xA﹣xB=2﹣n.
①当AC=BC时,
 =
= |n|,解得n=2(A、B两点重合,舍去)或n=﹣2;
|n|,解得n=2(A、B两点重合,舍去)或n=﹣2;②当AC=AB时,
 =2﹣n,解得n=0(B、C两点重合,舍去)或n=﹣
=2﹣n,解得n=0(B、C两点重合,舍去)或n=﹣ ;
;③当BC=AB时,
 |n|=2﹣n,
|n|=2﹣n,当n>0时,
 n=2﹣n,解得n=
n=2﹣n,解得n= ,
,当n<0时,﹣
 n=2﹣n,解得n=﹣
n=2﹣n,解得n=﹣ .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目

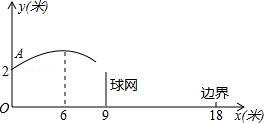

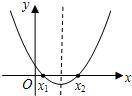
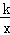 的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )
的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )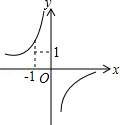
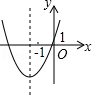
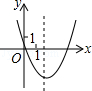

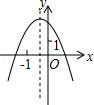
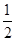 ,2)
,2)