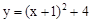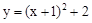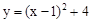��Ŀ����
��ͼ��������y=-x2+bx+c��x�ύ�ڵ�A��1,0����C����y���ڵ�B���Գ���x=-1��x�ύ�ڵ�D��
��1����������ߵĽ���ʽ��B��C������ꣻ
��2�����P��x��y���ǵڶ������ڸ��������ϵ�һ�����㣬��PBD�����ΪS����S����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��

��3����G��x�Ḻ�����ϣ��ҡ�GAB=��GBA����G�����ꣻ
��4����������������һ��Q�������QCA=��ABO,�����ڣ���ֱ��QC�Ľ���ʽ���������ڣ���˵������.
��1����������ߵĽ���ʽ��B��C������ꣻ
��2�����P��x��y���ǵڶ������ڸ��������ϵ�һ�����㣬��PBD�����ΪS����S����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��

��3����G��x�Ḻ�����ϣ��ҡ�GAB=��GBA����G�����ꣻ
��4����������������һ��Q�������QCA=��ABO,�����ڣ���ֱ��QC�Ľ���ʽ���������ڣ���˵������.
��1��y=-x2-2x+3��C��-3,0����B��0,3������2��S=��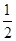 x2-
x2-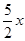 ��-3��x��0������3��G��-4,0����(4)���ڣ�
��-3��x��0������3��G��-4,0����(4)���ڣ�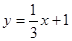 ����
����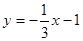 .
.
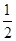 x2-
x2-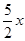 ��-3��x��0������3��G��-4,0����(4)���ڣ�
��-3��x��0������3��G��-4,0����(4)���ڣ�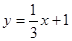 ����
����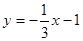 .
.�����������1���ȸ���������y=-x2+bx+c��x�ύ�ڵ�A��1��0�����Գ���Ϊx=-1���г�����b��c�ķ����飬�ⷽ�������b��c��ֵ���õ������ߵĽ���ʽΪy=-x2-2x+3���ٽⷽ��-x2-2x+3=0�����x��ֵ���õ�C������ꣻ��x=0����y=-x2-2x+3�����y��ֵ���õ�B������ꣻ
��2������P��PE��x���ڵ�E������S=S����PEOB-S��BOD-S��PDE���S����x�ĺ�����ϵʽ���ٸ��ݵ�P��x��y���ǵڶ������ڸ��������ϵ�һ�����㣬�ó��Ա���x��ȡֵ��Χ��
��3����G������Ϊ��a��0������a��0�����ݵȽǶԵȱߵó�GB=GA���ɴ��г�����a2+32=��1-a��2���ⷽ�����a��ֵ�����ɵõ�G�����ꣻ
��4���ȸ������к����Ķ���ó�tan��ABO=
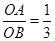 �����ڡ�QCA=��ABO���õ�tan��QCA=
�����ڡ�QCA=��ABO���õ�tan��QCA=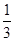 ������ֱ��б�ʵ������ֱ֪��QC��б��|k|=
������ֱ��б�ʵ������ֱ֪��QC��б��|k|=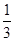 ����k=��
����k=��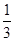 ���ɴ˿���ֱ��QC�Ľ���ʽΪy=
���ɴ˿���ֱ��QC�Ľ���ʽΪy=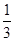 x+n����y=-
x+n����y=-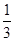 x+n��Ȼ��C�����꣨-3��0�����룬���n��ֵ�����ɵõ�ֱ��QC�Ľ���ʽ��
x+n��Ȼ��C�����꣨-3��0�����룬���n��ֵ�����ɵõ�ֱ��QC�Ľ���ʽ�����������(1) b=-2��c="3" ��C��-3,0����B��0,3��
(2)����P��PE��x���ڵ�E��
S=S����PEOB��S��BOD��S��PDE=
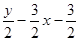 ��
����y=��x2-2x+3�����S=��
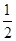 x2-x+
x2-x+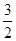 -
-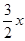 ��
��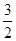 =��
=��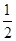 x2-
x2-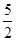 x��
x����-3��x��0��
��S����x�ĺ�����ϵʽΪ��S=��
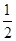 x2-
x2-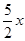 ��-3��x��0����
��-3��x��0������3��G��-4,0��
(4)����
ֱ��QC����ʽΪ
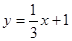 ����
����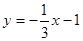 .
.
��ϰ��ϵ�д�
�����Ŀ
 ��ʾ������ͼ1�У�
��ʾ������ͼ1�У� ��ͼ2�У�
��ͼ2�У� .
. ��
�� ��
�� ��Ϊ��P���ڡ�ABC�ġ�������ꡱ������
��Ϊ��P���ڡ�ABC�ġ�������ꡱ������ ������ͼ3�У�����ABCD�ı߳�Ϊ2��
������ͼ3�У�����ABCD�ı߳�Ϊ2�� ����
���� ����G���ڡ�ABC�ġ�������ꡱ
����G���ڡ�ABC�ġ�������ꡱ Ϊ
Ϊ .��ͼ3�У�����֪��
.��ͼ3�У�����֪�� �����á����������������Ҳ������ʽ��ʾΪ��
�����á����������������Ҳ������ʽ��ʾΪ�� .
. ����D���ڡ�ABC�ġ�������ꡱ�� ��̽�����֣�
����D���ڡ�ABC�ġ�������ꡱ�� ��̽�����֣� �У���
���� ��
�� �ġ�������ꡱΪ
�ġ�������ꡱΪ ��
�� ��
�� ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�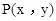 �ǵ�������������һ�㣬��ֱ��д����P����
�ǵ�������������һ�㣬��ֱ��д����P���� ����Q��������
����Q�������� �ϣ���
�ϣ��� ��ֵ��Сʱ����Q�ĺ�����.
��ֵ��Сʱ����Q�ĺ�����.
 ��
�� ���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C.���н��ۣ���
���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C.���н��ۣ���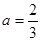 ����
����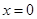 ʱ��
ʱ�� ����ƽ����x���ֱ��
����ƽ����x���ֱ�� ���������������ĸ����㣻��2AB=3AC�����д�����۵ĸ����ǣ� ��
���������������ĸ����㣻��2AB=3AC�����д�����۵ĸ����ǣ� ��


 CPD �����Ϊy. ������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ� ��
CPD �����Ϊy. ������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ� ��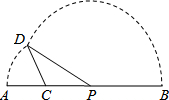
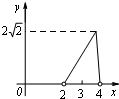 B.
B. 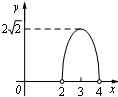 C.
C. 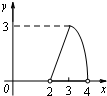 D.
D.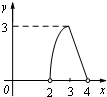
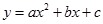 ��ͼ���У�����ͬѧ�۲�ó�������������Ϣ����1��
��ͼ���У�����ͬѧ�۲�ó�������������Ϣ����1��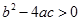 ����2��c>1����3��2a��b<0����4��a+b+c<0������Ϊ���д�����У�������
����2��c>1����3��2a��b<0����4��a+b+c<0������Ϊ���д�����У�������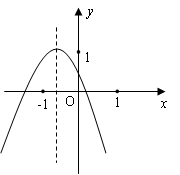
 ��Ϊ
��Ϊ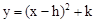 ����ʽ�����Ϊ�� ��
����ʽ�����Ϊ�� ��