题目内容
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知 球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?
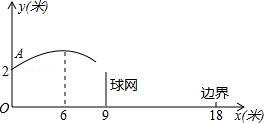
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

(1)y与x的关系式为:y=﹣ (x﹣6)2+2.6,
(x﹣6)2+2.6,
(2)球能过球网;会出界;
(3)若球一定能越过球网,又不出边界,h的取值范围是:h≥ .
.
 (x﹣6)2+2.6,
(x﹣6)2+2.6,(2)球能过球网;会出界;
(3)若球一定能越过球网,又不出边界,h的取值范围是:h≥
 .
.试题分析:(1)由h=2.6,球从O点正上方2m的A处发出,将点(0,2)代入解析式求出即可;
(2)当x=9时,y=
 (x﹣6)2+2.6=2.45>2.43;当y=0时,
(x﹣6)2+2.6=2.45>2.43;当y=0时, (x﹣6)2+2.6=0,得x=6+
(x﹣6)2+2.6=0,得x=6+ >18即可作出判断;
>18即可作出判断;(3)根据当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),以及当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2)时分别得出h的取值范围,即可得出答案.
试题解析:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=
 ,
,故y与x的关系式为:y=
 (x﹣6)2+2.6,
(x﹣6)2+2.6,(2)当x=9时,y=
 (x﹣6)2+2.6=2.45>2.43,
(x﹣6)2+2.6=2.45>2.43,所以球能过球网;
当y=0时,
 (x﹣6)2+2.6=0,
(x﹣6)2+2.6=0,解得:x1=6+
 >18,x2=6﹣
>18,x2=6﹣ (舍去)
(舍去)故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
 ,
,解得
 ,
,此时二次函数解析式为:y=
 (x﹣6)2+
(x﹣6)2+ ,
,此时球若不出边界h≥
 ,
,当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
 ,
,解得
 ,
,此时球要过网h≥
 ,
,故若球一定能越过球网,又不出边界,h的取值范围是:h≥
 .
.
练习册系列答案
相关题目

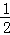 x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ; (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;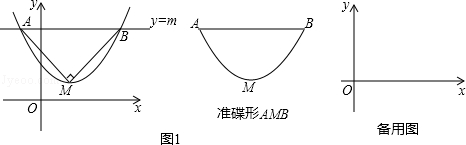
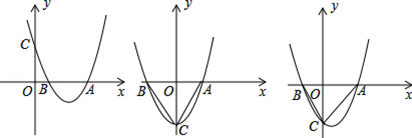
 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
. ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
. ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: 中,点
中,点 ,
, 的“面积坐标”为
的“面积坐标”为 ,
, 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;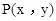 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.



