题目内容
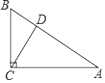
【题目】如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,∠A=30°,BD=1,则AB的值是( ).
A.1B.2C.3D.4
【答案】D
【解析】
在直角三角形ABC中,由∠A的度数求出∠B的度数,在直角三角形BCD中,可得出∠BCD度数为30°,根据直角三角形中,30°所对的直角边等于斜边的一半,得到BC=2BD,由BD的长求出BC的长,在直角三角形ABC中,同理得到AB=2BC,由BC的长即可求出AB的长.
∵△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,又CD⊥AB,
∴∠BCD=30°,
在Rt△BCD中,∠BCD=30°,BD=1,
可得BC=2BD=2,
在Rt△ABC中,∠A=30°,BC=2,
则AB=2BC=4.
故选:D.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目