Question

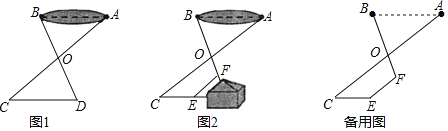
【题目】如图，在Rt△ABC中，∠C＝90°，Rt△BAP中，∠BAP＝90°，已知∠CBO＝∠ABP，BP交AC于点O，E为AC上一点，且AE＝OC.

(1)求证:AP＝AO;

(2)求证:PE⊥AO.

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）根据等角的余角相等证明即可；
（2）过点O作OD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CO=DO，利用“SAS”证明△APE和△OAD全等，根据全等三角形对应角相等可得∠AEP=∠ADO=90°，从而得证．

（1）证明：∵∠C=90°，∠BAP=90°
∴∠CBO+∠BOC=90°，∠ABP+∠APB=90°，
又∵∠CBO=∠ABP，
∴∠BOC=∠APB，
∵∠BOC=∠AOP，
∴∠AOP=∠APB，
∴AP=AO；
（2）证明：如图，过点O作OD⊥AB于D，

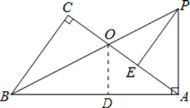
∵∠CBO=∠ABP，
∴CO=DO，
∵AE=OC，
∴AE=OD，
∵∠AOD+∠OAD=90°，∠PAE+∠OAD=90°，
∴∠AOD=∠PAE，
在△AOD和△PAE中，

，
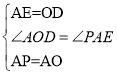∴△AOD≌△PAE（SAS），
∴∠AEP=∠ADO=90°
∴PE⊥AO．