题目内容
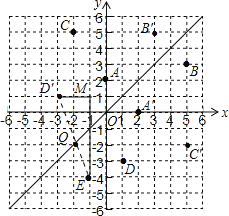
【题目】如图，在平面直角坐标系中，直线
是第一、三象限的角平分线.
（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：
___________、
___________；
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点
关于第一、三象限的角平分线的对称点
的坐标为___________（不必证明）；
（3）已知两点
、
，试在直线L上画出点Q，使点Q到D、E两点的距离之和最小，求QD+QE的最小值．
【答案】（1）
,
.（2）
（3）
【解析】
（1）根据对称轴为第一、三象限的角平分线，结合图形得出B′、C′两点坐标；
（2）由（1）的结论，并与B、C两点坐标进行比较，得出一般规律；
（3）由轴对称性作出满足条件的Q点，结合勾股定理，得出结论．
（1）如图，由点关于直线y=x轴对称可知：B'（3，5），C'（5，-2）．
故答案为：（3，5），（5，-2）；
（2）由（1）的结果可知，
坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为 （b，a）．
故答案为：（b，a）；
（3）由（2）得，D（1，-3）关于直线l的对称点D'的坐标为（-3，1），连接D'E交直线l于点Q，此时点Q到D、E两点的距离之和最小，D'E=
=
，
∴QD+QE的最小值为：．
练习册系列答案
相关题目
