题目内容
【题目】对于平面直角坐标系中的任意一点P(a,b),我们定义:当k为常数,且k≠0时,点P′(a+![]() ,ka+b)为点P的“k对应点”.
,ka+b)为点P的“k对应点”.
(1)点P(﹣2,1)的“3对应点”P′的坐标为 ;若点P的“﹣2对应点”P′的坐标为(﹣3,6),且点P的纵坐标为4,则点P的横坐标a= ;
(2)若点P的“k对应点”P′在第一、三象限的角平分线(原点除外)上,求k值;
(3)若点P在x轴的负半轴上,点P的“k对应点”为P′点,且∠OP'P=30°,求k值.
【答案】(1)(﹣![]() ,﹣5),﹣1;(2)k=1;(3)k=
,﹣5),﹣1;(2)k=1;(3)k=![]() 或﹣
或﹣![]() .
.
【解析】
(1)根据点P的“k对应点”的定义列式计算,得到答案;
(2)根据第一、三象限的角平分线上的点的横纵坐标相等计算;
(3)根据点P的“k对应点”的定义表示出P′点的坐标,根据直角三角形的性质、正切的定义计算即可.
解:(1)﹣2+![]() =﹣
=﹣![]() ,﹣2×3+1=﹣5,
,﹣2×3+1=﹣5,
则点P(﹣2,1)的“3对应点”P′的坐标为(﹣![]() ,﹣5),
,﹣5),
∵点P的“﹣2对应点”P′的坐标为(﹣3,6),点P的纵坐标为4,
∴﹣2a+4=6,
解得,a=﹣1,即点P的横坐标a=﹣1,
故答案为:(﹣![]() ,﹣5);﹣1;
,﹣5);﹣1;
(2)∵点P′在第一、三象限的角平分线(原点除外)上,
∴a+![]() =ka+b,
=ka+b,
整理得,(ka+b)(1﹣k)=0,
由题意得,ka+b≠0,
∴1﹣k=0,
解得,k=1;
(3)如图
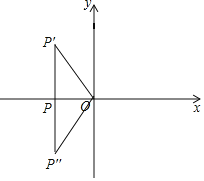
∵点P在x轴的负半轴上,
∴设点P的坐标为(a,0),
则点P的“k对应点”为P′点的坐标为(a,ka),
∴PP′⊥x轴,
∵∠OP'P=30°,
∴![]() =tan30°,
=tan30°,
∴![]() =
=![]() ,
,
解得,k=±![]() ,
,
则点P在x轴的负半轴上,点P的“k对应点”为P′点,∠OP'P=30°时,k=![]() 或﹣
或﹣![]() .
.

练习册系列答案
相关题目