题目内容
【题目】综合与实践
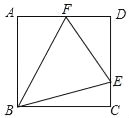
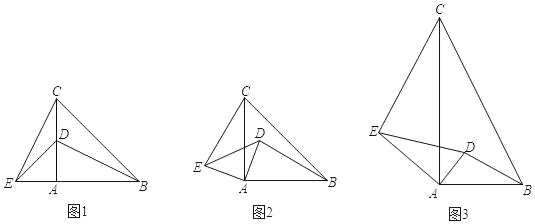
问题情境:如图1,在数学活动课上,老师让同学们画了等腰Rt△ABC和等腰Rt△ADE,并连接CE,BD.
操作发现:(1)当等腰Rt△ADE绕点A旋转,如图2,勤奋小组发现了:
①线段CE与线段BD之间的数量关系是 .
②直线CE与直线BD之间的位置关系是 .
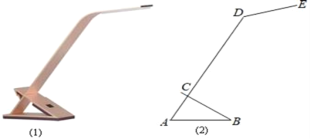
类比思考:(2)智慧小组在此基础上进行了深入思考,如图3,若△ABC与△ADE都为直角三角形,∠BAC=∠DAE=90°,且AC=2AB,AE=2AD,请你写出CE与BD的数量关系和位置关系,并加以证明.
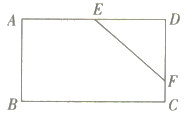
拓展应用:(3)创新小组在(2)的基础上,又作了进一步拓展研究,当点E在直线AB上方时,若DE∥AB,且AB=![]() ,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
【答案】(1)EC=BD; BD⊥EC;(2) CE=2BD,CE⊥BD.理由见解析;(3)4.
【解析】
(1)如图2中,延长BD交AC于点O,交EC于H.证明△EAC≌△DAB(SAS),即可解决问题.
(2)结论:CE=2BD,CE⊥BD.如图3中,延长BD交AC于点O,交EC于点H.证明△ABD∽△ACE,即可解决问题.
(3)如图4中,当DE∥AB时,设DE交AC于H,易证AC⊥DE.求出EH,CH,理由勾股定理即可解决问题.
(1)如图2中,延长BD交AC于点O,交EC于H.
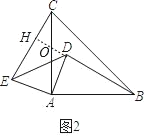
∵AE=AD,AC=AB,∠EAD=∠CAB=90°,
∴∠EAC=∠DAB,
∴△EAC≌△DAB(SAS),
∴EC=BD,∠ECA=∠ABD,
∵∠ABD+∠AOB=90°,∠AOB=∠COH,
∴∠ECA+∠COH=90°,
∴∠CHO=90°,
∴BD⊥EC,
故答案为EC=BD,BD⊥EC.
(2)结论:CE=2BD,CE⊥BD.
理由:如图3中,延长BD交AC于点O,交EC于点H.

∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AC=2AB,AE=2AD,
∴![]() ,
,
∴△ABD∽△ACE,
∴![]() ,
,
∴CE=2BD,∠ABD=∠ACE,
∵∠ABD+∠AOB=90°,∠AOB=∠COH,
∴∠ECA+∠COH=90°,
∴∠CHO=90°,
∴BD⊥EC.
(3)如图4中,当DE∥AB时,设DE交AC于H,易证AC⊥DE.

∵AE=2AD,AD=1,
∴AE=2,DE=![]() ,
,![]() ,
,![]() ,
,
∵AC=2AB,AB=![]() ,
,
∴CH=AC﹣AH=![]() ,
,
在Rt△ECH中,EC=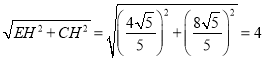 .
.