题目内容
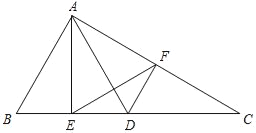
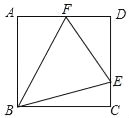
【题目】如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是_____.
【答案】3
【解析】
根据正方形的性质得BA=BC,∠ABC=90°,则可把△BAE绕点B顺时针旋转90°得到△BCG,如图,根据旋转的性质得∠BCG=∠BAF=90°,∠FBG=∠ABC=90°,AF=CG,所以点G、C、F共线,再利用“SAS”证明△BFE≌△BGE,得到∠FEB=∠GEB,设正方形的边长为2a,CE=x,则AF=DF=a,CG=AF=a,DF=2a﹣x,EF=EG=x+a,在Rt△DEF中,利用勾股定理得到a2+(2a﹣x)2=(x+a)2,解得x=![]() a,然后在Rt△BCF中,根据正切的定义得tan∠BEC=
a,然后在Rt△BCF中,根据正切的定义得tan∠BEC=![]() =3,即tan∠FEB的值为3.
=3,即tan∠FEB的值为3.
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
把△BAF绕点B顺时针旋转90°得到△BCG,如图,
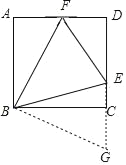
∴∠BCG=∠BAF=90°,∠FBG=∠ABC=90°,AF=CG,
∴点G、C、E共线,
∵∠EBF=45°,
∴∠GBE=45°,BG=BF,
在△BEF和△BGE中,
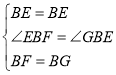 ,
,
∴△BEF≌△BGE(SAS),
∴∠FEB=∠GEB,
设正方形的边长为2a,CE=x,则AF=DF=a,CG=AF=a,DF=2a﹣x,EF=EG=x+a,
在Rt△DEF中,∵DF2+DE2=EF2,
∴a2+(2a﹣x)2=(x+a)2,
解得x=![]() a,
a,
在Rt△BCE中,
tan∠CEB=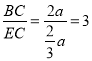 ,
,
∴tan∠FEB=3.
故答案为3.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】一家健身俱乐部收费标准为180元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次收费(元) |
A类 | 1500 | 100 |
B类 | 3000 | 60 |
C类 | 4000 | 40 |
例如,购买A类会员年卡,一年内健身20次,消费![]() 元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
A.购买A类会员年卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
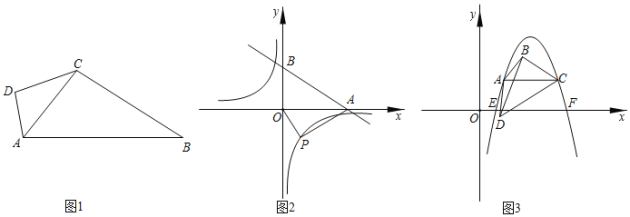
【题目】如图1,M是圆中![]() 上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
下面是小帅的探究过程,请补充完整:
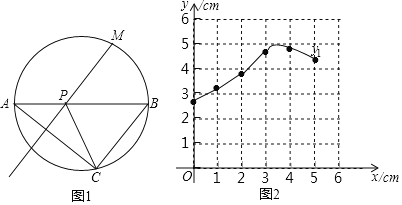
(1)按照表中自变量x的值进行取点,画图、测量,分别得到了y1、y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.55 | 3.15 | 3.95 | 4.76 | 4.95 | 4.30 |
y2/cm | 2.55 | 2.64 | 2.67 |
| 1.13 | 2.55 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:在点P的运动过程中,当AC与PC的差为最大值时,AP的长度约为 cm.