题目内容
【题目】如图,AB是⊙O的直径,P是BA延长线上一点,过点P作⊙O的切线,切点为D,连接BD,过点B作射线PD的垂线,垂足为C.

(1)求证:BD平分∠ABC;
(2)如果AB=6,sin∠CBD![]() ,求PD的长.
,求PD的长.
【答案】(1)详见解析;(2) ![]()
【解析】
(1)连接OD,证明OD∥BC,再由OB=OD证明∠OBD=∠ODB,进而得结论;
(2)连接AD,根据圆周角定理得到∠ADB=90°,解直角三角形得到BD=4![]() ,BC=
,BC=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)证明:连接OD,如图1,
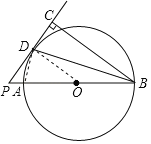
∵PD是⊙O的切线,
∴OD⊥PC,
∵BC⊥PC,
∴OD∥BC,
∴∠ODB=∠CBD,
∵OB=OD,
∴∠ODB=∠OBD,
∴∠CBD=∠OBD,
即BD平分∠ABC;
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵sin∠CBD=sin∠ABD![]() ,AB=6,
,AB=6,
∴AD=2,
∴BD=4![]() ,
,
∵sin∠CBD![]() ,
,
∴CD![]() ,
,
∴BC![]() ,
,
∵OD∥BC,
∴△PDO∽△PCB,
∴![]() ,
,
∴ ,
,
∴PD![]() .
.

练习册系列答案
相关题目
【题目】一家健身俱乐部收费标准为180元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次收费(元) |
A类 | 1500 | 100 |
B类 | 3000 | 60 |
C类 | 4000 | 40 |
例如,购买A类会员年卡,一年内健身20次,消费![]() 元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
A.购买A类会员年卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡