题目内容
【题目】甲、乙两地之间有一条笔直的公路,快车和慢车分别从甲、乙两地同时出发,沿这条公路匀速相向而行,快车到达乙地后停止行驶,慢车到达甲地后停止行驶,已知快车速度为![]() .下图为两车之间的距离
.下图为两车之间的距离![]() 与慢车行驶时间
与慢车行驶时间![]() 的部分函数图像.
的部分函数图像.
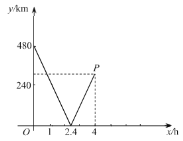
(1)甲、乙两地之间的距离是______km;
(2)点![]() 的坐标为(4,____),解释点
的坐标为(4,____),解释点![]() 的实际意义.
的实际意义.
(3)根据题意,补全函数图像(标明必要的数据).
【答案】(1)480;(2)320,实际意义见解析;(3)见解析
【解析】
(1)观察图象,两车之间的距离与慢车的行驶时间之间的感受图象;
(2)观察图象,根据慢车行驶2.4小时时,两车之间的距离为0,求出慢车的行驶的速度,再求出当x=4时的路程;
(3)根据两地之间的距离480km,画出图象即可.
(1)从图象可以看出,两地之间的距离是480km;
故答案为:480;
(2)从图象中可以看出,慢车行驶2.4小时时,两车之间的距离为0,即相遇,
∴慢车的速度为:480÷2.4-120=200-120=80,
∴当x=4时,快车已经到达乙地,此时两车之间的距离就是慢车行驶的路程,
∴当x=4时,两车之间的距离为:4×80=320,
∴点P的纵坐标为:320,实际意义为:两车出发了4小时后,相距320km,此时快车到达了乙地,
故答案为:320;
(3)慢车距离甲地还有480-320=160km,
需要用时:160÷80=2(小时),
∴2小时后到达甲地,
∴图象如图所示.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目