题目内容
【题目】【问题发现】
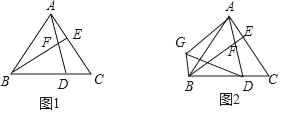
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

【答案】(1)AC垂直平分BD(2)四边形FMAN是矩形(3)BD′的平方为16+8![]() 或16–8
或16–8![]()
【解析】试题分析:(1)根据AB=AD、CB=CD可知点A、C在线段BD的垂直平分线上,从而可得;
(2)连接AF,判断出DF是AB的垂直平分线,从而可得∠FMA=90![]() ,同理可得∠FNA=90
,同理可得∠FNA=90![]() ,再根据∠MAN=90
,再根据∠MAN=90![]() ,即可判断出四边形FMAN为矩形;
,即可判断出四边形FMAN为矩形;
(3)分逆时针旋转与顺时针旋转两种情况分别讨论即可得.
试题解析:(1)∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∵点A、点C是不同的点,
∴AC⊥BD,
故答案为:垂直;
(2)猜想:四边形FMAN是矩形,理由如下:
连接AF,在Rt△ABC中,∵点F为BC的中点,
![]() AF=BF,
AF=BF,
在等腰三角形ADB中,AD=BD,
![]() FD垂直平分AB,
FD垂直平分AB,![]() ∠FMA=90
∠FMA=90![]() ,
,
同理可得∠FNA=90![]() ,又∵∠MAN=90
,又∵∠MAN=90![]() ,
,
![]() 四边形FMAN为矩形;
四边形FMAN为矩形;
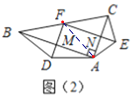
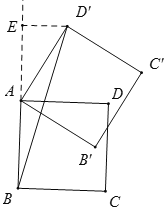
(3)当逆时针旋转60度时,如图,过点D′作D′⊥AB,交BA延长线于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8+4
)2+12=8+4![]() ;
;
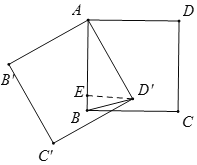
当顺时针旋转60度时,如图,过点D′作D′⊥AB,交BA于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8-4
)2+12=8-4![]() ,
,
综上,BD′2的值为8+4![]() 或8-4
或8-4![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案