题目内容
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C 在数轴上相距 28 个长度单位,动点 P 从点 A 出发, 以 2 单位/秒的速度沿着“折线数轴”的正方向运动,从点 O 运动到点 B 期间速度变为原来的一半; 点 P 从点 A 出发的同时,点 Q 从点 C 出发,以 1 单位秒的速度沿着“折线数轴”的负方向运动,当 点 P 到达 B 点时,点 P、Q 均停止运动. 设运动的时间为 t 秒. 问:
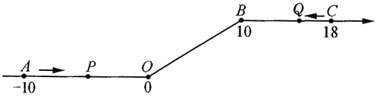
(1)当 t=3s 时,点 P 和点 O 在数轴上相距 个长度单位; 当 t=7.5s 时,点 P 和点 O 在数轴上相距 个长度单位; 当 t=9s 时,点 P 和点 Q 在数轴上相距 个长度单位.
(2)当 P、Q 两点相遇时,求出相遇时间及相遇点 M 所对应的数是多少?
(3)是否存在某一时刻使得 P、O 两点在数轴上相距的长度与 Q、B 两点在数轴上相距的长度相等? 若存在,请直接写出 t 的取值;若不存在,请说明理由.
【答案】(1)4; 2.5;6;(2)![]() 分,
分,![]() ;(3)t的值为2、6.5、11或17.
;(3)t的值为2、6.5、11或17.
【解析】
(1)根据路程等于速度乘以时间,可得点P运动的路,从而可求出点P与点O相距的距离;用总路程减去点P与点Q的运动路程之和即可得到点 P 和点 Q 在数轴上相距的长度单位;
(2)根据题意可以列出相应的方程,从而可以求得相遇时间及相遇点M所对应的数;
(3)根据PO与BQ的长度相等,可得方程,根据解方程,可得答案.
(1)当 t=3s 时,点P和点O在数轴上相距10-2×3=4个长度单位;当 t=7.5s 时,点 P 和点 O 在数轴上相距(7.5-10÷2)×1=2.5个长度单位;当t=9s时,点P和点Q在数轴上相距28-10-(9-10÷2)×1-8×1=6长度单位;
(2)设经过a秒,P、Q两点相遇,
10+(a-5)×(2÷1)+a×1=28,
解得,a=![]() ,
,
即P、Q 两点相遇时间为:![]() (分)
(分)
则点M所对应的数是:28-10-![]() =
=![]() ,
,
即点M所对应的数是![]() ;
;
(3)P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等有4种可能:
①动点Q在CB上,动点P在AO上,则:8-t=10-2t,解得:t=2.
②动点Q在CB上,动点P在OB上,则:8-t=(t-5)×1,解得:t=6.5.
③动点Q在BO上,动点P在OB上,则:2(t-8)=(t-5)×1,解得:t=11.
④动点Q在OA上,动点P在BC上,则:10+2(t-15)=t-13+10,解得:t=17.
综上所述:t的值为2、6.5、11或17.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?