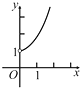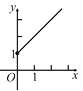��Ŀ����
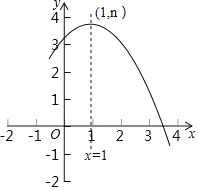
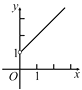
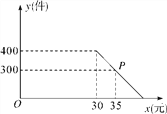
����Ŀ��ij�̵깺��һ������Ϊ20Ԫ/����������Ʒ����һ���£����������50%�ļ۸���ۣ��۳�400�����ڶ����£��̵����ڲ�����ԭ�ۼ۵Ļ����Ͻ��мӼ����ۣ��������۾��飬������۵��ۻᵼ���������ļ��٣�������y(��)�����۵���x(Ԫ)�Ĺ�ϵ��ͼ��ʾ��
(1)��y��x֮��ĺ�������ʽ��
(2)�ڶ����µ����۵��۶�Ϊ����Ԫʱ���ɻ�����������������Ƕ��٣�
���𰸡���1��y��x֮��ĺ�������ʽΪy����20x��1000.��2���ڶ����µ����۵��۶�Ϊ35Ԫʱ���ɻ������������������4500Ԫ��
�������������������1������ͼ�����ô���ϵ����������⼴�ɵã�
��2����������=������������������г���������ʽ�������ö��κ��������ʼ��ɵ�.
���������(1)��y��x֮��ĺ�������ʽΪy��kx��b��
����(30��400)��(35��300)����y��kx��b�е�![]() �����
�����![]() ��
��
��y��x֮��ĺ�������ʽΪy����20x��1000��
(2)��ڶ����µ�����ΪwԪ������֪��w��(x��20)y��(x��20)(��20x��1000)����20x2��1400x��20000����20(x��35)2��4500��
����20��0���൱x��35ʱ��wȡ���ֵ�����ֵΪ4500.�ʵڶ����µ����۵��۶�Ϊ35Ԫʱ���ɻ������������������4500Ԫ��

����Ŀ������С������������ÿ��13.1Ԫ�ļ۸����ij�ֹ�Ʊ1000�ɣ��ù�Ʊ���ܵ��ǵ����(�������ֱ�ʾ��ǰ--���ǻ������Ԫ)���±�(��λ:Ԫ):
���� | һ | �� | �� | �� | �� |
ÿ���ǵ� | -0.3 | 0 | -0.1 | +0.2 | +0.1 |
(1)�����������ÿ��__________Ԫ��ͼ���ÿ��Ԫ_________��
(2)���С��������������ǰ��ȫ����Ʊ��������������������?