题目内容
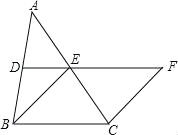
【题目】如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.
(1)求证:∠ABE=∠CAD;
(2)如图2,以AD为边向左作等边△ADG,连接BG.
ⅰ)试判断四边形AGBE的形状,并说明理由;
ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).
【答案】(1)详见解析;(2)ⅰ)四边形AGBE是平行四边形,证明详见解析;ⅱ)![]() .
.
【解析】
(1)只要证明△BAE≌△ACD;
(2)ⅰ)四边形AGBE是平行四边形,只要证明BG=AE,BG∥AE即可;
ⅱ)求出四边形BGAE的周长,△ABC的周长即可;
(1)证明:如图1中,
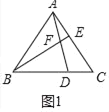
∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
∵AE=CD,
∴△BAE≌△ACD,
∴∠ABE=∠CAD.
(2)ⅰ)如图2中,结论:四边形AGBE是平行四边形.
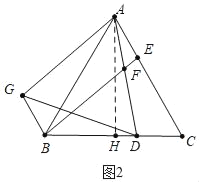
理由:∵△ADG,△ABC都是等边三角形,
∴AG=AD,AB=AC,
∴∠GAD=∠BAC=60°,
∴△GAB≌△DAC,
∴BG=CD,∠ABG=∠C,
∵CD=AE,∠C=∠BAE,
∴BG=AE,∠ABG=∠BAE,
∴BG∥AE,
∴四边形AGBE是平行四边形,
ⅱ)如图2中,作AH⊥BC于H.
∵BH=CH=![]()
∴![]()
∴![]()
∴四边形BGAE的周长=![]() ,△ABC的周长=3(k+1),
,△ABC的周长=3(k+1),
∴四边形AGBE与△ABC的周长比=![]()

练习册系列答案
相关题目