题目内容
【题目】某体育用品商店为了解3月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.
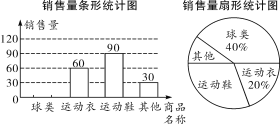
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按3月份球类商品销售量购进球类商品,含篮球、足球、排球三种,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如下表:
类别 | 篮球 | 足球 | 排球 |
进价(单位:元/个) | 50 | 30 | 20 |
预售价(单位:元/个) | 70 | 45 | 25 |
求y与x之间满足的函数关系式;
(3)该商店综合考虑各种因素,预计每种球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)之间满足的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.
【答案】(1)见解析;(2)![]() ;(3)①
;(3)①![]() (
(![]() ,且x为整数);②此时购进篮球20个,足球60个,排球40个
,且x为整数);②此时购进篮球20个,足球60个,排球40个
【解析】
(1)补全条形统计图如解图:
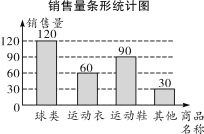
【解法提示】∵从销售量条形统计图可以看出,运动衣的销售量为60件,从销售量扇形统计图可以看出,运动衣的销售占比为![]() ,∴总销量为
,∴总销量为![]() (件),又∵从销售量扇形统计图可以看出,球类的销售占比为
(件),又∵从销售量扇形统计图可以看出,球类的销售占比为![]() ,∴球类的销量为
,∴球类的销量为![]() (件).
(件).
(2)根据题意该商店准备购进球类商品120个,预计恰好用完进货款共3600元,购进篮球x个,足球y个,则购进排球![]() 个,则
个,则
![]() ,
,
故y与x之间满足的函数关系式为![]() ;
;
(3)①∵预计每种球销售超过60个后,这种球就会产生滞销,
而假设所购进篮球、足球、排球能全部售出,
∴![]() ;
;![]() ,即
,即![]() ;
;![]() ,
,
即![]() ,
,
∴![]() ,且x为整数,
,且x为整数,
![]()
![]()
![]()
![]()
![]() ,
,
∴预估利润P(元)与x(个)之间满足的函数关系式为:
![]() (
(![]() ,且x为整数);
,且x为整数);
②当![]() 时,P的值最大,最大值为
时,P的值最大,最大值为
![]() (元),
(元),
则![]() ,
,
即此时购进篮球20个,足球60个,排球40个.

【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
![]() .小云所住小区5月1日至30日的厨余垃圾分出量统计图:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
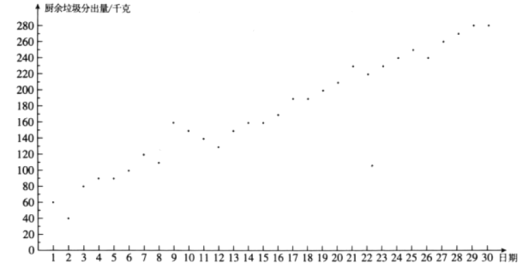
![]() .小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为 (结果取整数)
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为![]() 5月11日至20日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为![]() ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为![]() .直接写出
.直接写出![]() 的大小关系.
的大小关系.
【题目】为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的![]() ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
车速v(km/h) | 40 | 50 |
刹车距离s乙(m) | 12 | 17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
【题目】从2018年12月初开始,某地环保部门连续一年对![]() 两市的空气质量进行监测,将
两市的空气质量进行监测,将![]() 天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,
天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,![]() 个月的空气污染指数如下:
个月的空气污染指数如下:
![]()
![]()
整理、描述数据:
空气质量
按如表整理、描述这两市空气污染指数的数据:
城市 | 空气质量为优 | 空气质量为良 | 空气质量为轻微污染 |
|
|
|
|
|
说明:空气污染指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气污染指数
空气污染指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
分析数据:
两市的空气污染指数的平均数、中位数、众数如下表所示;
城市 | 平均数 | 中位数 | 众数 |
|
|
| |
|
|
|
请将以上两个表格补充完整:
得出结论:可以推断出 市这一年中环境状况比较好,理由_____.(至少从两个不同的角度说明推断的合理性)