题目内容
【题目】县政府计划建设一项水利工程,工程需要运送的土石方总量为![]() (单位:
(单位:![]() ),某运输公司承担了运送土石方的任务.
),某运输公司承担了运送土石方的任务.
(1)运输公司平均运输速度v(单位:![]() 天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
(2)这个运输公司共有80辆卡车,每天可运输土石方为![]() (单位:
(单位:![]() ),公司完成全部运输任务需要多长时间?
),公司完成全部运输任务需要多长时间?
(3)当公司以问题(2)中的速度工作了30天后,由于工程进度的需要,剩下的运输任务必须在20天内完成,则运输公司至少要增加多少辆卡车?
【答案】(1)![]() ;(2)公司完成全部运输任务需要60天;(3)运输公司至少要增加40辆卡车.
;(2)公司完成全部运输任务需要60天;(3)运输公司至少要增加40辆卡车.
【解析】
(1)由总量=vt,求出v即可;
(2)把v的值代入计算即可求出t的值;
(3)设需要增加a辆卡车,每辆卡车每天运输土石方为![]() m3,求出前30天与后20天的土石方确定出解析式,即可求出a的最小值.
m3,求出前30天与后20天的土石方确定出解析式,即可求出a的最小值.
(1)根据题意得:![]() ,
,
![]() ;
;
(2)当![]() 时,
时,
![]() ,
,
答:公司完成全部运输任务需要60天;
(3)设需要增加a辆卡车,每辆卡车每天运输土石方为![]() ,
,
![]() 前30天运输土石方为:
前30天运输土石方为:![]() ,
,
![]() 后20天运输土石方为:
后20天运输土石方为:![]() .
.
设30天后的每天平均运输速度为![]() ,所需时间为
,所需时间为![]() ,
,
![]() ,
,
由反比例函数的性质可知,![]() 随着
随着![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,![]() 的最小值是40.
的最小值是40.
答:运输公司至少要增加40辆卡车.

【题目】例 如图①,李老师设计了一个探究杠杆平衡条件的实验:在一个自制的类似天平的仪器的左边固定托盘![]() 中放置一个重物,在右边活动托盘
中放置一个重物,在右边活动托盘![]() (可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘
(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘![]() 与点
与点![]() 的距离
的距离![]() ,观察活动托盘
,观察活动托盘![]() 中砝码的质量
中砝码的质量![]() 的变化情况.实验数据记录如表:
的变化情况.实验数据记录如表:
| 10 | 15 | 20 | 25 | 30 |
| 30 | 20 | 15 | 12 | 10 |
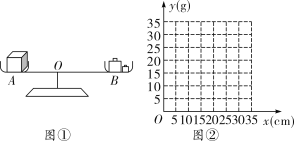
(1)把表中![]() 的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测![]() 与
与![]() 之间的函数关系,求出函数关系式;
之间的函数关系,求出函数关系式;
(3)当砝码的质量为![]() 时,活动托盘
时,活动托盘![]() 与点
与点![]() 的距离是多少?
的距离是多少?
【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 |
| 2 | 90 |
电热水壶 | 35 | 1 |
|
合计 | 8 | 280 |
(1)直接写出![]() ________,
________,![]() ________;
________;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,若买的垃圾桶的数量比买字画的数量多2个,则甲居民买字画多少个?
【题目】某体育用品商店为了解3月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.
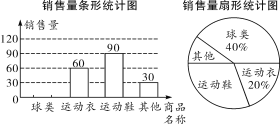
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按3月份球类商品销售量购进球类商品,含篮球、足球、排球三种,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如下表:
类别 | 篮球 | 足球 | 排球 |
进价(单位:元/个) | 50 | 30 | 20 |
预售价(单位:元/个) | 70 | 45 | 25 |
求y与x之间满足的函数关系式;
(3)该商店综合考虑各种因素,预计每种球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)之间满足的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.