题目内容
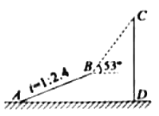
【题目】某兴趣小组为了测量大楼![]() 的高度,先沿着斜坡
的高度,先沿着斜坡![]() 走了
走了![]() 米到达坡顶点
米到达坡顶点![]() 处,然后在点
处,然后在点![]() 处测得大楼顶点
处测得大楼顶点![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的坡度为
的坡度为![]() ,点
,点![]() 到大楼的距离
到大楼的距离![]() 为
为![]() 米,求大楼的高度
米,求大楼的高度![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】大楼的高度![]() 为52米
为52米
【解析】
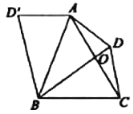
过点B作BE⊥AD于点E,作BF⊥CD于点F,在Rt△ABE中,根据坡度![]() 及勾股定理求出BE和AE的长,进而由三个角是直角的四边形是矩形判断四边形BEDF是矩形,得到BF和FD的长,再在Rt△BCF中,根据∠CBF的正切函数解直角三角形,得到CF的长,由CD=CF+FD得解.
及勾股定理求出BE和AE的长,进而由三个角是直角的四边形是矩形判断四边形BEDF是矩形,得到BF和FD的长,再在Rt△BCF中,根据∠CBF的正切函数解直角三角形,得到CF的长,由CD=CF+FD得解.
解:如下图,过点B作BE⊥AD于点E,作BF⊥CD于点F,
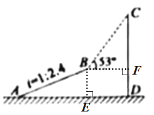
在Rt△ABE中,AB=52,
∵![]()
∴tan∠BAE=![]() =
=![]() ,
,
∴AE=2.4BE,
又∵BE2+AE2=AB2,
∴BE2+(2.4BE)2=522,
解得:BE=20,
∴AE=2.4BE=48;
∵∠BED=∠D=∠BFD=90°,
∴四边形BEDF是矩形,
∴FD=BE=20,BF=ED=AD-AE=72-48=24;
在Rt△BCF中,
tan∠CBF=![]() ,
,
即:tan53°=![]() =
=![]()
∴CF=![]() BF=32,
BF=32,
∴CD=CF+FD=32+20=52.
答:大楼的高度![]() 为52米.
为52米.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 |
| 2 | 90 |
电热水壶 | 35 | 1 |
|
合计 | 8 | 280 |
(1)直接写出![]() ________,
________,![]() ________;
________;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,若买的垃圾桶的数量比买字画的数量多2个,则甲居民买字画多少个?
【题目】某体育用品商店为了解3月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.
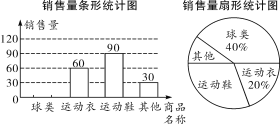
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按3月份球类商品销售量购进球类商品,含篮球、足球、排球三种,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如下表:
类别 | 篮球 | 足球 | 排球 |
进价(单位:元/个) | 50 | 30 | 20 |
预售价(单位:元/个) | 70 | 45 | 25 |
求y与x之间满足的函数关系式;
(3)该商店综合考虑各种因素,预计每种球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)之间满足的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.