题目内容
【题目】为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的![]() ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
车速v(km/h) | 40 | 50 |
刹车距离s乙(m) | 12 | 17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
【答案】(1)s甲=![]() v,s乙=
v,s乙=![]() v2+
v2+![]() v;(2)乙车的最长刹车距离为84米;(3)v甲>v乙,甲车超速.
v;(2)乙车的最长刹车距离为84米;(3)v甲>v乙,甲车超速.
【解析】
(1)根据“甲车的刹车距离s甲是车速v的![]() ”可以求得s甲与车速v的函数关系式.设s乙=k1v+k2v2,把(40,12),(50,17.5)分别代入该函数解析式,列出关系系数的方程组,通过解方程组求得它们的值;
”可以求得s甲与车速v的函数关系式.设s乙=k1v+k2v2,把(40,12),(50,17.5)分别代入该函数解析式,列出关系系数的方程组,通过解方程组求得它们的值;
(2)利用(1)中的函数关系式,结合抛物线的性质来求其顶点坐标即可;
(3)根据(1)中的函数关系式可以求得甲、乙的速度.然后结合限速80km/h判定它们是否超速.
(1)依题意得:s甲=![]() v,
v,
∵反应距离与车速v成正比,制动距离与车速v2成正比
∴设s乙=k1v+k2v2,
由题意得:![]() ,
,
解得: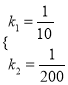 ,
,
∴s乙=![]() v2+
v2+![]() v;
v;
(2)∵对称轴为v=-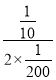 =-10,
=-10,
∴当0<v≤120 时,s乙随v的增大而增大,即当v=120时,s乙最大值=![]() ×14400+
×14400+![]() ×120=84
×120=84
∴乙车的最长刹车距离为84米.
(3)∵甲车的刹车距离超过16m,但小于18m,
∴16<![]() v<18,
v<18,
即80<v<90,
又∵乙车的刹车距离是24m
∴![]() v2+
v2+![]() v=24,
v=24,
解得v1=60,v2=-80(舍去),
∵限速80km/h
∴甲车超速.

【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
【题目】某体育用品商店为了解3月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.
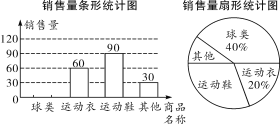
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按3月份球类商品销售量购进球类商品,含篮球、足球、排球三种,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如下表:
类别 | 篮球 | 足球 | 排球 |
进价(单位:元/个) | 50 | 30 | 20 |
预售价(单位:元/个) | 70 | 45 | 25 |
求y与x之间满足的函数关系式;
(3)该商店综合考虑各种因素,预计每种球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)之间满足的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8